李某是一起机场杀人案的犯罪嫌疑人。警方在调取高速路口监控录像时发现:案发前两小时, 李某驾车行驶在高速公路, 在通往机场的路口驶离高速 (记为证据E1) 。此高速出口距机场大约40分钟车程, 是这条高速通往机场的最近出口。那么, 如何评价证据E1?这个证据对于待证事实“李某去了机场” (记为H1) 的证明力有多大?如果监控录像显示在此路口驶离高速的汽车中, 只有为数不多的汽车驶向机场, 又该如何评价证据E1?

此外, 警方在案发现场找到一块血迹, 鉴定人员对这块血迹的DNA分子进行结构分析, 并从李某身上也提取一块血迹样本进行DNA分析。经过比对和鉴定, 这两块血迹的DNA结构匹配度非常高 (记为证据E2) 。那么, 又如何评价证据E2?它对于待证事实“案发现场的血迹来源于李某” (记为H2) 的证明力有多大?倘若经过比对和鉴定发现这两块血迹的DNA结构匹配度较低 (记为证据E3) , 是否可以认定证据E3对待证事实H2的证明力很小?

以上问题在司法实践中经常遇到。目前, 法庭在认定和接受证据时, 基本上采用自由心证的评价模式。为了防止法官滥用自由裁量权, 自由心证必须遵循经验法则和逻辑法则, 而概率论就是理性的逻辑准则。因此, 基于贝叶斯概率的似然率是一种评价证据力度的科学化方法, 能够为法官的心证推理过程建模, 更好地促进法官心证形成过程的规范化。本文将从贝叶斯模型的研究视角对证据评价进行深入探讨, 以期通过一种概率方法解决证据评价体系所面临的上述问题。

证明力源于证据的相关性及其关联程度, 若要评价证据的证明力一定离不开相关性, 所以我们首先阐述相关性的含义。沃尔顿 (Douglas N.Walton) 从论证理论角度作了如此阐释:当且仅当存在从一个命题作为起点到另一个命题作为终点的推理链条时, 一个命题才与另一个命题相关。这种使用逻辑工具给法律意义上的相关性进行定义性描述与威格摩尔 (John H.Wigmore) 的相关性理论息息相关。威格摩尔认为, 两个命题具有相关性, 是指其中一个命题作为论证另一个命题链条中的一部分, 具有潜在的“证明力”^[1]。他主张, 相关性是一个逻辑问题, 而非严格意义上的法律问题, 可以定义为“证据事实”与待证事实 (审判中待证的命题) 相互之间的一种联系。只要证据事实具有证明力, 即如果它能够用于证明或者证伪案件中所争议的待证事实, 那么它就具有相关性^[2]20。

既然证明力是与相关性密切联系的一个概念, 那么二者究竟存在什么内在关系?

为此, 有学者进一步提出“证据的证明力是由该证据与案件主要事实之间的关联形式和性质所决定, 抽象地说, 证明力的高低与其关联的远近成反比。有关联就有证明价值, 无关联则无证明价值, 关联近则证明价值高, 关联远则证明价值低”^[3]140。质言之, 如果一个证据不能使我们改变对待证事实的概率评价, 那么就不能把其看成支持或反对该事实的证据;只有那种使我们增加或降低对某一事实 (这一待证事实对认定整个案件有重要的意义) 概率评价的证据, 才是值得考察的证据。那么, 如何理解改变人们对某一事实之概率评价的证据?现在通过以下两种情形来解释。

第一, 理想证据, 即当待证事实为真时, 这个证据总是出现, 而当它为假时, 这个证据从未出现。要证明某个事实为真, 我们总会想法设法找到理想证据, 因其能够强烈促使人们改变先前对事实的概率评价。例如, 要证明甲某受贿巨额资金6000万元, 我们会尽力找到其受贿的证据, 如在他名下账户里有6000万元进账凭证, 或在他家里搜查到6000万元现金等。如果发现这样理想的证据, 则可以大大提高人们对“甲某犯受贿罪”为真的概率评价。遗憾的是, 在现实生活中, 理想证据却很难发现, 甚至不存在。例如, 要证明乙某对丙某实施了强奸行为, 理想证据就是在丙某体内获取乙某精液。然而这种证据很难找到, 因为罪犯极可能采取安全措施, 不会在丙某体内留下自己的精液证据。

第二, “无用证据”, 即毫无区分度的证据, 因其不能促使人们改变任何概率评价。例如我们想证实张某说谎, 可以对其进行测谎实验。如果在测谎过程中对张某的所有表现不作任何区分, 那么像“张某在呼吸”这样的证据则毫无意义, 因为所有未撒谎的人在测谎过程中也在呼吸。尽管呼吸是所有撒谎者的共同特征, 但呼吸也是未撒谎者之特征。所以, 呼吸对于区分撒谎者与未撒谎者就是无用证据。此外, 在人体细胞中, 绝大多数的DNA是没有区分度的, 这也是每个人都有脑袋和腿的原因。因此, 这种类型的DNA鉴定将对案件中凶手身份的认定毫无作用^[4]18~20。

在现实世界, 我们很难收集到理想证据。所以, 生活中常常遇到这样的证据, 其在待证事实为真时比它为假时更易发生或更易不发生, 即为好证据。质言之, 好证据必然使得人们对待证事实之概率评价发生实质性变化。例如, 在测谎过程中, 当且仅当皮肤电阻图谱在撒谎时比不撒谎时更容易紊乱, 皮肤电阻图谱紊乱才被视为撒谎证据。如果在撒谎人群中有80%的人会出现皮肤电阻图谱紊乱, 而在不撒谎人群中只有10%的人出现皮肤电阻图谱紊乱, 那么, 撒谎者在测谎过程中出现皮肤电阻图谱紊乱的可能性是未撒谎者的8倍。因此, 皮肤电阻图谱紊乱就是测定被测人撒谎的好证据, 这将提高人们对被测人“撒谎”为真的概率评价。

从上述的讨论, 可以推出评价证据的证明力, 就是审查证据能否改变以及在何种程度上改变人们对待证事实的概率评价。本文认为, “能否改变”指涉的是证据的相关性, “在何种程度上改变”指涉的是证明力。如果我们用数值刻画, 那么相关性是“一个二进制的值, 即一项证据要么相关要么不相关”, 而证明力是“一个连续的值, 在从很弱 (甚至不存在) 到极强 (事实上具有结论性) 的区间内变动”^[5]999。实际上, 评价证据的证明力揭示了证据的相关性与证明力之间的内在联系。因此, 若我们能够利用某种方法直接查明某项证据的证明力大小, 显然也就证成了相关性概念所包含的证明力要素, 因为只要有任何证明力就能满足相关性要求。而作为测度证明价值的模型, 似然率方法对于评价证据相关性和证明力再合适不过。

(一) 不确定命题信念度的定量测度

以似然率方法测度相关性和证明力的原因在于, 我们可以使用概率数值计算命题的信念度。现实世界存在着大量不确定的现象。例如, 明天是否下雨?犯罪嫌疑人是否为真凶?不确定现象可以分为两类:一类是还未发生的事情, 它将来出现的结果不可预测。如投掷一枚骰子时, 可能出现六种不同点数, 人们无法确定性地知悉其出现的点数。另一类是已经发生的事实, 其结果本身已经确定, 比如犯罪嫌疑人本身要么是真凶, 要么不是真凶;但囿于人们认知能力的局限性, 根据现有资料信息, 通常无法完全确定其结果。在诉讼证明中, 待证假设或事实的不确定性就属于第二类情形。某些证据的真假也具有不确定性, 尤其是科学证据, 如鉴定意见“现场采集的DNA与嫌疑犯的DNA相匹配”, 这类证据不确定性是由统计计算的不确定性造成, 也属于第二类情形。这里, 待证假设或事实以及上述证据都可以用“命题”形式统一刻画。易言之, 这些命题为真具有不确定性。

基于自己的经验、知识背景, 不同人对不确定命题可能持有不同的信念, 所确定命题为真的程度称为“个人信念度”, 简称“信念度”。一般情况下, 人们习惯用诸如“很强”、“很弱”等模糊语词来表述对某一命题的信念度。但司法实务中, 尤其是在法官或陪审团权衡证据证明力时, 如果能够用相对精确的数值度量命题的信念度, 将有助于明确地揭示自由心证的形成过程。概率是对不确定现象发生可能性的度量, 因此, 用概率数值测量信念度为不二之选。“以贝叶斯观点来看, 某事物成立的概率即对于该事物的信念度”^[6]。概率数值取0到1之间的任意实数。命题概率值为0, 说明该命题为假, 表示它不可能发生。命题概率值为1, 表示人们相信此命题为真。一般情形下, 命题的概率评价都取值于0和1之间。例如概率值为0.7表示人们以70%的信念相信此命题为真, 而30%的信念相信其否定命题为真。

信念度的概率数值化, 对进行不确定推理具有理性的指导作用。数字本身并不重要, 重要的是概率数值可使我们通过计算机程序来处理复杂的推理, 并且, 借助概率演算的规则能够建模推理规则, 还可以回答诸如这样的问题:假设命题A和命题B相互关联, 当命题B信念度很高的情形下, 命题A的信念度如何?如果降低对命题B的信念度, 命题A的信念度又将如何变化?

我们还可以用另一种方式———几率来表示命题的信念度。一个命题的几率是此命题为真的概率与其否定命题为真的概率之比, 它表示该命题为真的概率较其为假的概率高或者低多少倍。用数学公式可表示为:

其中, O (A) 表示命题A为真的几率, P (A) 表示命题A为真的概率, P (劭A) 表示其否定命题劭A为真的概率, 且P (劭A) =1-P (A) 。

根据公式 (1) , 命题的概率和几率可以相互转化。如果命题A为真的概率为0.7, 说明相信该命题为真的几率为0.7/ (1-0.7) =7∶3。反过来, 如果相信命题A为真的几率为7∶3, 则该命题为真的概率为0.7。

命题信念度的“概率表示”和“几率表示”本质上相同, 都是定量刻画命题为真的程度。不过, 采用几率方法能够更好地表达贝叶斯公式, 在理解层面上更加自然, 从而清楚地阐释证据的相关性和证明力。并且很多情况下我们是无法直接计算某个命题为真的概率, 但是可以大致估算其为真的概率与为假的概率之比。例如, 根据笔迹专家的长期执业经验, 他可以估算“某种笔迹属于伪造”这一命题为真概率是为假概率的十倍, 然后根据两者的比值间接计算该命题为真的概率数值。

(二) 基于贝叶斯公式的信念度更新关系

由于“可能性”可以表示人们的主观信念度, 所以, 变换一种角度, 相关的证据能够使人们对命题的信念度发生改变, 改变的力度越大表示证据的证明力越强。因此, 我们可以用信念度更新的情况来刻画证据的相关性和证明力。又由于我们可以运用概率数值计算信念度, 所以将证据相关性和证明力问题转化为概率理论问题。

概率理论的基础是条件概率规则。所谓“条件概率”即给定某一条件之后, 某一事件的发生概率。如P (A|B) , 它表示B为真的条件下命题A为真的概率, 即对于A为真的信念度。在证据法领域中, 我们要关注的是证据 (E) 和命题 (H) 之间的概率关系, 因此, 常用H和E分别替代A和B, 即E为真的条件下命题H为真的概率。

某些案件中, 我们可以直接根据经验和常识来判断, 证据E的出现是否使得争议事实H为真变得更加可能或更加不可能。例如被告人被指控攻击了邻居 (H) 。证据表明, 他拥有无暴力的声誉 (E) 。生活经验告诉我们, 攻击邻居者在拥有无暴力声誉的人之中所占的比例会低于他们在全体人口之中所占的比例。因此, 给定无暴力声誉 (E) , 被告人攻击邻居这一命题 (H) 的概率P (H|E) 会小于不考虑E时命题H的概率P (H) 。证据改变了攻击概率, 即P (H|E) <P (H) , 这说明证据对于命题H具有相关性和证明力^[5]996。

但是, 许多案件并不能直接断定这种概率改变, 而必须从命题与证据之间的紧密度出发反推证据的证明力和相关性。因为, 某一命题与某一证据联系越紧密, 该证据出现时, 该命题越可能为真。例如, 如果经验表明某一命题 (如气温低于零度) 出现时, 某一证据 (如下雪) 出现的概率较高, 那么当该证据出现时, 运用回溯论证可以反推该命题亦更可能为真 (下雪表明气温低于零度) 。易言之, 我们通过P (E|H) 反推P (H|E) , 然后再如前所述将其与P (H) 进行比较。贝叶斯公式以较为正式的形式确认了这种反推关系^[7]。

一般情形下, 对于某一观察到的现象 (E) , 可以提出两种不同的解释H和劭H。例如观察到下雪, 可以提出两个互斥的命题:一个是气温等于或低于零度, 另一个是气温高于零度。司法实践中, E通常表现为观察到或获得的证据材料, H和劭H分别为对E进行解释的命题。对于这两种命题, 实践中用不同的符号进行表述, 如Hp和Hd (原告提出的主张和被告提出的主张) 、H和~H、H和劭H (这三组均表示命题和其否定命题, 其概率之和等于1) 。E与H和劭H之间的关系可以用如下形式的贝叶斯公式表示:

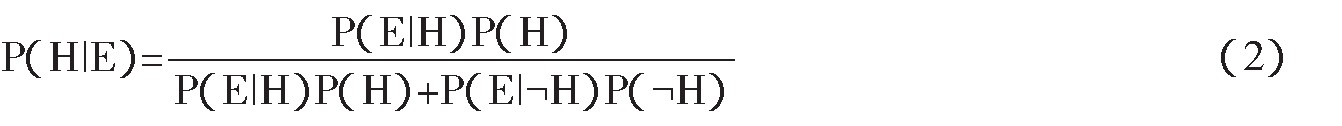
其中, P (H) 和P (劭H) 称为“先验概率”, 它表示不知晓证据E之前命题H和劭H为真的概率。P (H|E) 称为命题H的“后验概率”, 它表示在给定证据E为真的条件下命题H为真的概率。P (E|H) 、P (E|劭H) 分别称为命题H和劭H相对于证据E的“似然度”, 分别表示基于现已认知的背景信息, 在命题H或劭H为真的条件下证据E为真的概率。

贝叶斯公式是概率统计中运用观察到的现象对概率分布之主观判断 (即先验概率) 进行修正, 以此得出后验概率的标准方法。其实质是一种理性决策程序:始于“先验概率”, 接着收集大量证据材料, 然后通过科学的方法将二者结合形成“后验概率”。贝叶斯公式的重要意义在于, 它提供了一个信念度更新的规则。

详言之, 利用贝叶斯公式, 证据信息获取的过程按照时间顺序可归结为两个步骤。第一步, 在时刻t₀, 人们基于已有信息, 对命题H为真以及其否定命题劭H为真各有一个信念度, 分别记为P₀ (H) 和P₀ (劭H) , 这两个概率值也被称为先验概率。例如在一起强奸杀人案中, 警方在被害人体内提取到A图谱DNA, 对此可提出两个命题:犯罪嫌疑人甲某是本案的杀人犯 (H) , 犯罪嫌疑人甲某不是本案的杀人犯 (劭H) 。在比对DNA证据之前, 基于对嫌疑犯的了解以及证人证言等其他证据, 法官对这两个命题会初步形成一定的概率认识。第二步, 在时刻t₁, 人们发现证据E (A图谱DNA来自犯罪嫌疑人甲某) 为真, 那么此时对命题H为真的信念度P₁ (H) 就等于命题H的后验概率, 即P₁ (H) =P₀ (H|E) 。后验概率是经由一定的推论关系取得的, 这种关系以基于定量的似然度数值和贝叶斯公式确定, 即公式 (2) 。

(一) 似然率的构建

在贝叶斯公式中, 先验概率P (H) 和P (劭H) 主观性很强, 由法官根据自己的经验以及案件中提交的其他证据作出评价, 因此很难对它们赋予精确数值。这样, 利用公式 (2) 难以计算出后验概率P (H|E) ;进而也就不能判断当证据E出现时命题H为真的概率。为解决这一问题, 人们通过概率运算将贝叶斯公式转化为如下形式:

其中, 等号左边式子称为命题H为真的“后验几率” (posterior odds) , 表示证据E支持命题H为真的程度;等号右边第一个式子称为命题H为真的“先验几率” (prior odds) , 表示在考虑证据E之前命题H为真的概率相对于命题劭H为真的概率之比;右边第二个式子叫做“似然率”。公式 (3) 可用文字表述为:

从中, 我们得出似然率公式为:

似然率度量的是证据E对命题H为真的证明力, 它对于后验几率有重要的影响。案件进入庭审阶段时, 裁判者根据现有的证据资料, 并结合自己的经验, 对案件事实或案情某些片段都会有一个先验概率评价。随着庭审的深入、新证据的呈现, 裁判者会不断地更新其概率评价, 其数学依据就是贝叶斯公式。正如不确定命题的信念度有概率形式和几率形式, 贝叶斯公式也有相应的这两种表述, 即公式 (2) 和 (3) 。美国著名法官、学者波斯纳 (Richard A.Posner) 在《法官如何思考》一书中也给出了贝叶斯公式的表达, 即:

其中, Ω是几率, 该等式左边是表示某假设H为真的后验几率, 该等式右边的Ω (H) 是先验几率。x是在调查过程中获得的新信息, P是概率并且该等式右边的P (x|H) /P (x|~H) 是概率之比, 即如果命题H为真时x将被观察到的概率与如果命题~H为真时x将被观察到的概率之比。倘若P (x|H) 和P (x|~H) 这两个概率相同, 新信息x则没有改变后验几率, 这种情形表示二者概率之比等于1。公式 (6) 被波斯纳称为贝叶斯定理最简化的版本^[8]66。

该公式与前述公式 (3) 对于贝叶斯公式的刻画本质上具有一致性。首先, 公式 (6) 中获得的新信息x即为通过观察得到的证据材料E。其次, Ω (H|x) 表示在已知信息x为真的情形下, 命题H为真的几率, 即为P (H|E) 与P (劭|E) 之比。接着, Ω (H) 表示命题H为真的先验几率, 即为P (H) 与P (劭H) 的比值。

值得一提的是, 有学者认为“波斯纳给出的这个贝叶斯公式和常见的贝叶斯公式看上去有明显不同”, 如果按照“在《法官如何思考》一书中, 他把Ω和P都叫做概率”, 那么所得到的贝叶斯公式“显然是错误的”, 所以提出“波斯纳是否写错了贝叶斯公式”的观点;并在文中进一步“澄清一个可能困扰《法官如何思考》读者的数学问题, 因为波斯纳把他的贝叶斯公式中的Ω和P都叫做概率, 却没有直接指明它们的定义是不同的, 也没有显式地给出它们的定义”^[9]。事实上, 波斯纳在书中并没有把Ω和P都叫做概率, Ω称为几率, P称为概率。几率和概率是数学领域中两个不同的术语, 二者之间的区别已在本文中第三部分详细阐释, 这里不再赘述。因此, Ω和P不会给读者带来困惑, 波斯纳本人也毋需明确的显式给出其定义。

(二) 似然率在证据评价中的作用

在判断证据对待证事实是否相关时, 传统上主要借助于所谓的“逻辑与经验”, 或者“事物的发展过程”。例如美国证据法学家塞耶 (James B.Thayer) 指出, “法律并未提供相关性的测试标准。对此, 它含混地提及逻辑和一般经验, 假设其裁判者知悉推理的种种原则”^[10]265。另一位著名的证据学家克劳斯 (Sir R.Cross) 指出, “根据事物的发展过程, 两项事实相互之间具有非常紧密的联系, 其中一项事实单独或与其他事实相结合能够证明另一项事实过去、现在或将来的存在或不存在, 或使其具有盖然性”^[11]18。加拿大最高法院也指出, “决定可采性时, 首先考察寻求被采信的证据是否相关。这是一个将逻辑和经验适用于个案情形的问题” ⁽¹⁾ 。

那么, 什么是“逻辑与经验”或“事物的发展过程”?正如前所述, 事实上, 判断相关性时既包含逻辑的成分, 也包含经验的成分。有学者认为, 一个事实是否与另一项事实相关, 可以归属于三段论问题:以提出的证据事实作为小前提, 以所要证明的待证事实作为结论。例如小前提是甲某出生在农村, 寻求的结论是甲某偷盗了乙某的手表。从小前提得出结论, 需要有一个得到事实认定者接受的大前提:这一大前提要求保证从小前提推出结论。如果存在这样的大前提, 就可以从小前提得出结论, 从而小前提事实与结论事实就是相关的^[12]。

判断一个大前提是否成立时需要借助于经验。当然“经验”并不限于常识, 还包括人们通过长期观察总结出来的规律、通过社会调查或实证研究得出的结论等。例如没有任何证据表明农村出生的人比城市出生的人更倾向于偷盗;相反, 社会调查或者心理学研究成果可能揭示出, 曾经被多次判决盗窃罪的人比一般人更倾向于盗窃。

而似然率或者后验概率的计算, 正是基于人们的经验总结, 即通过大量的研究和观察建立起证据与命题 (待证事实) 之间的紧密联系 (似然度) 。似然度的建立实际上提供了判断相关性的大前提, 即后验概率P (偷盗|曾经被判处盗窃罪) ;这种似然度越高, 说明事实认定者越能够接受这一联系作为大前提, 协助从本案小前提得出结论, 如甲某曾多次被判处盗窃罪蕴涵甲某更可能偷盗乙某的手表。

传统方式下的“经验”是一种模糊的、不精确的、粗糙的经验, 只能概括性地告诉我们某个事实与另一事实之间存在足够的关联, 从而提供了可以进行三段论推理的大前提。与之不同, 似然率则将这种联系 (相对) 明确地数字化, 运用数学方法表征证据的证明力, 贝叶斯公式甚至提供了据此计算出个案中以证据事实证明待证事实的程度———后验概率。因此, 似然率方法作为一种量化模型, 将人们日常实践中潜在的、隐性的知识转化为显性知识。这种精确到数值的模型, 比经验和感性认识更加可靠, 能够规范法官确认案件事实的思维过程, 是证据评价体系中的最佳方法。

案例一:在本文开头所述机场杀人案中, 对证据E1的评价应作如下推理:如果李某去机场, 那他很可能从这个路口驶离高速;如果李某不去机场, 那他几乎不会从这个路口驶离高速。这样, P (E1|H1) 远比P (E1|劭H1) 概率值大, 因此, 证据E1对待证事实H1为真具有显著的证明力, 是一个好证据。“监控录像显示在此路口驶离高速的汽车中, 只有少数汽车去了机场”, 这个信息不会影响对证据E1的证明力评价, 因为只要“去机场的汽车在此路口驶出高速的比例”远大于“不去机场的汽车在此路口驶出高速的比例”, 证据E1的似然率仍然很大, 同样具有显著的证明力。另外, 仅凭两块血迹中的DAN分子结构匹配度很高, 无法推定证据E2对待证事实H2有很强证明力, 还需要从人群中随机选取第三者的DNA与犯罪现场的DNA做比对, 如果匹配度也很高, 则证据E2的证明力较弱, 如果匹配度都很低, 则证据E2的证明力很强。同样, 仅凭两块血迹中的DAN分子结构匹配度很低, 也无法推定证据E3对待证事实H2的证明力很小, 如果从人群中随机选取第三者的DNA与犯罪现场的DNA做比对, 并且匹配度更低, 则证据E3对待证事实H2也有较强的证明力。

案例二:著名的20世纪大审判———辛普森 (Orenthal James Simpson) 杀妻案, 在美国引起了轩然大波。艾伦 (Alan Dershowitz) 律师对辛普森的无罪释放起到决定性作用, 其中有一段是他运用数学概率进行辩护的证言。巧舌如簧的艾伦为了说明证据“辛普森经常虐待妻子 (E) ”对待证假设“辛普森杀死自己的妻子 (H) ”的证明力微弱, 进行了如下论证:美国每年有400万妇女被丈夫殴打、虐待, 可是美国每年只有1432名妇女被丈夫杀死, 这说明那些长期虐待妻子的男人最后出手杀人的概率也就将近1/2500, 因此, 以“辛普森经常虐待妻子 (E) ”来说明“辛普森杀死自己的妻子 (H) ”是不可靠的。

实际上, 艾伦的辩词是有破绽的, 他评价证据“辛普森经常虐待妻子 (E) ”, 所进行的概率演算是不合理的, 其计算方法并不能反映证据E对假设“辛普森杀死自己的妻子 (H) ”的证明力。正确方法应该是再结合其他数据来计算证据E的似然率。我们还需要获取两个数据, 一是在1432名被丈夫杀害的妇女中, 有多少妇女长期遭受过丈夫的虐待?比如有1289人;二是当时美国有多少对夫妻?比如有0.79亿对 ⁽¹⁾ 。基于这些数据, 就可以进行如下合理的计算:

由上面的计算可知, 证据E的似然率为18, 对假设H具有“适度的证据支持” ⁽²⁾ 。然而, 按照艾伦的方法, 证据E的似然率仅为:1/2500&#247; (1-1/2500) =0.0004, 对假设H有“强证据反对”。显然, 艾伦的结论违背常理。根据常识、经验、直觉, 我们都能判断证据E倾向于支持假设H为真, 只是支持力度强弱程度的问题, 而按照艾伦计算, 却得到证据E强烈反对支持假设H为真这一荒谬结论。由此, 当年宣告“辛普森无罪释放”的判决, 并不能反映案件的真实情况。

从上面的分析可以看出, 按照传统的比例方法来评价证明力存在很大的缺陷, 因其毫无理论支持, 结论也是不可靠的。正确评价证明力的方法是基于贝叶斯公式的似然率。现在, 似然率模型已经广泛应用于司法实务中, 法庭科学家经常运用数值概率的DNA证据 (如血液证据) , 统计学方面的专家受邀就给定案件情况发生某种犯罪的概率进行作证。这种方法为刻画和量化证据与待证事实之间的推论关系提供形式框架, 并在法庭科学领域获得显著效果。然而, 在应用似然率过程中, 还需解决一些现实问题。

如在本文中, 我们考虑的只是关于案件事实的两种假设, 即待证假设H及其否定命题劭H。这是有助于阐释似然率方法所做的一种简化处理。但这种简化处理必然引起一些问题。因为否定命题劭H可能包含许多个、甚至无穷多个子假设, 而这些子假设与所讨论证据的联系可能各不相同, 这种简化处理的方式却将所有这些子假设合并在一起, 同等对待每个子假设与证据的联系。我们仍以DNA证据为例, 以证据E表示“犯罪嫌疑人的DNA图谱与犯罪现场提取血迹的DNA图谱非常匹配”, 以假设H表示“犯罪现场找到的血迹来源于犯罪嫌疑人”, 那么其否定命题可分解为相当多个子假设, 包含这个血迹产生之前活着的所有人。每个子假设的先验概率是不一样的, 生活在被害人周围或与被害人有交往的人实施犯罪的可能性要比其他人高。因此, 这种简化的处理方式对于事实认定不可避免地会带来一定风险。为了达到“排除合理怀疑”的证明标准, 调查人员和决策者需要考虑就某个给定证据材料, 找出多个备选替代假设。

那么, 在这么多的备选假设下, 如何用似然率方法来评价证据, 即所谓的“多个备选假设”问题?目前学者们也在致力于解决这个问题。如法尓曼 (Richard D.Firedman) 提出了一个“分批处理”的解决方案, 其核心思想是:如果对于一些假设H_i, 当它们为真时, 证据E为真的概率相同或相差很小, 即各假设H_i的似然度P (E|H_i) 相等或相差甚小, 则可以把这些假设整体合并, 看成一个假设;另外还可以排除那些先验概率非常低的假设。这样处理后, 就可以大大减少备选假设的个数。但这种思路有两个缺陷:一是依赖于先验概率的计算, 而先验概率有时往往难以获得准确数值;二是计算复杂度很高^[13]。

相关性是证据可采的必要条件, 证据只有具有相关性才有可能纳入法庭调查。证明力反映的是证据与待证命题相关程度, 相关程度越高, 则证明力越强, 反之, 相关程度越低, 则证明力越弱。因此, 本文提出证据的相关性和证明力实际上是指证据能够使法官比无此证据时更加相信命题为真及其程度强弱。简言之, 相关的证据可以使法官对命题为真发生改变, 改变的程度越大说明证明力越强。而基于贝叶斯定理的似然率方法, 与判断证据相关性和证明力的传统方法深相契合, 并拥有悠久和深厚的概率论基础, 可以使之更加精确和明确化, 从而为法官评价证据提供理论证成和逻辑支持。

司法实践证明, 似然率方法在评价证据相关性和证明力方面均担当着重要角色, 是评价法庭科学证据最适当的贝叶斯模型。但由于似然率是相关领域专家经过长期实践、搜集大量数据而得到, 其工作量复杂而繁重, 并且它在适用过程中尚存在一些亟待解决的问题, 因此, 似然率需要多学科、多领域的专家相互合作, 不断地完善数据库, 才能得到合理的计算结果, 为证明力和相关性提供坚实的基础。在不久的将来, 我们相信似然率方法一定能够获得更大的发展, 其在证据评价体系中的应用也将更加广泛。

[1]D.N.Walton.Argumentation and Theory of Evidence[J].New Trends in Criminal Investigation and Evidence, 2000, (2) .

[2]Douglas N.Walton.Legal Argumentation and Evidence[M].State College:The Pennsylvania State University Press, 2002.

[3]何家弘, 刘品新.证据法学[M].北京:法律出版社, 2005.

[4]Bernard Robertson, G.A.Vignaux.Interpreting Evidence:Evaluating Forensic Science in The Courtroom[M].Chichester:John Wiley and Sons, 1995.

[5]Kenneth S.Broun, et al.Mc Cormick on Evidence (7th ed.) [M].Minnesota:Thomson/West, 2013.

[6]Anders Nordgaard, BirgittaRasmusson.The Likelihood Ratio as Value of Evidence-More than a Question of Numbers[J].Law, Probability&Risk, 2012, (4) .

[7]David H.Kaye.Likelihoodism, Bayesianism, and a Pair of Shoes[J].Jurimetrics, 2012, (1) .

[8]Richard Posner.How Judges Think[M].Cambridge:Harvard University Press, 2010.

[9]秦裕林, 葛岩, 林喜芬.波斯纳写错了贝叶斯公式吗?[J].交大法学, 2016, (4) .

[10]James Bradley Thayer.A Preliminary Treatise on Evidence at the Common Law[M].Boston:Little, Brown&Co., 1898.

[11]Sir R.Cross.Evidence (5th edition) [M].London:Butterworth&Co Publishers Ltd, 1979.

[12]Robert Margolis.The Concept of Relevance:In the Evidence Act and the Modern View[J].Singapore Law Review, 1990, (11) .

[13]Richard D.Firedman.Assessing Evidence[J].Michigan Law Review, 1996, (6) .

1 Graat v The Queen, 144 DLR (3d) 269, 1982.

2 经查数据, 1994年美国人口总数约3.16亿。根据美国年龄结构的分布, 20岁-50岁人占人口总数的50%左右, 即约有1.58亿人, 从而推出有约0.79亿对夫妻。

3 根据学者伯德尔斯提供的似然率数值与相应证明力等级表得出“适度的支持”。参见A.P.A. Broeders:Some observations on the use of probability scales in forensic identification, Forensic Linguistics, Volume 6, Number 2 (December 1999) , pp.228-241.

(原载《湖北大学学报》2018年06期)