【杜国平】括号表示法:一种中国式表示法
提要:逻辑常项是各种逻辑系统研究的核心,使用合适的方式表示逻辑常项,可以为逻辑研究提供良好的技术工具和清晰的呈现方式。根据逻辑常项符号表示法的产生和发展历程,可以将其归纳为三种形态:自然语言表示法、符号表示法和形式化表示法。逻辑常项表示法的变迁,不仅决定着逻辑形态的呈现形式,而且决定着逻辑研究的持续和深入发展。中置法和前置法是国际逻辑学界通行的两种主要的逻辑常项表示法,与之不同,作者受舍弗(H. M. Sheffer)函数和张清宇先生相关工作的启发,提出了一种新的逻辑常项表示法——括号表示法。在该表示法中,表示逻辑常项的符号只有一对左右括号。作者阐明在任意给定的逻辑系统中,只要使用一对括号就可以定义出该系统的所有逻辑常项,彰显了括号表示法强大的归约功能和表达功能。作者还证明了括号表示法其形式语言表达的唯一性。在此基础上,作者阐明:比起中置法,括号表示法表达更简洁;比起波兰表示法,括号表示法表达更清晰。括号表示法是一种整体表示法,是由中国学者提出并系统构建的符号表示法,因此也可以称为中国式表示法。
逻辑学是研究推理有效性的学问。在具体的逻辑系统中,推理的有效性又集中体现于逻辑常项的推理有效性,因之,逻辑常项是逻辑研究的核心。使用恰当的符号表示逻辑常项,可以为逻辑研究提供良好的技术工具和清晰的呈现方式。如何创新逻辑常项的符号表示法,为逻辑研究提供更加多元、更加适用的工具是逻辑研究的重要课题之一。本文拟在简要归纳分析不同形态逻辑表示法的基础上,提出一种仅仅使用一对括号就可以表达所有逻辑常项的符号表示法,揭示其与中置法和前置法的表达差异,并阐明其强大的表达功能和基本表达特征。
一、逻辑研究的核心对象
不同逻辑系统研究不同范围内的逻辑。亚里士多德的词项逻辑主要研究简单性质命题之间的推理关系,命题逻辑主要研究以命题为基本单位的若干命题之间的推理关系,谓词逻辑则主要研究以个体词和谓词为对象的各种量词之间的推理关系。
根据范围的不同,现代逻辑研究一般首先要创制足以表达该范围内研究对象的符号,即构建形式语言。在命题逻辑中,需要三类基本的符号:一类是表达各种不同命题的符号,通常用小写字母加下标的形式表示,如p1、p2等等;一类是描述诸命题之间联系的符号,即命题联接词符号,如否定符号┐、蕴涵符号→等等;一类是确定命题之间结合先后顺序的辅助性符号,如左右括号( )等等。
在一阶谓词逻辑中,为了足以表达命题内部结构的诸对象,一般需要如下几组符号:
1.表达命题内部结构的符号。(1)表达个体对象的符号;(2)表达个体对象性质或者诸个体对象之间关系的符号;(3)表达具有某种性质或者关系的诸对象范围的符号,即量词符号。
2.表达诸命题之间联系的命题联接词符号。
3.表达命题间联系之先后顺序的符号。
由命题逻辑和一阶谓词逻辑可以看出,形式语言实际上主要包括三类符号,第一类是描述研究范围内特定语言对象的符号,如命题逻辑中的命题符号、一阶谓词逻辑中的个体对象符号和谓词符号等;第二类是描述特定范围内具有推理属性的符号,如命题逻辑中的各种命题联接词符号、谓词逻辑中的量词符号、模态逻辑中的模态词符号等;第三类是其他辅助性符号,如描述命题之间结合先后顺序的符号(通常使用各种括号表示)、个体词之间的间隔符号(通常使用逗号等表示)等。第一类符号主要是描述特定范围内的研究对象,第二类符号描述的是特定范围内具有推理功能的逻辑对象。不难看出,真正表达各种推理功能的是第二类符号,即通常所说的逻辑常项。所以,逻辑常项是不同逻辑系统的形式语言所要表达的关键对象。
逻辑研究的核心是推理,不同的逻辑系统研究的是不同逻辑常项的推理结构和推理功能。因此,具体到各种逻辑系统之中,实际上逻辑常项是逻辑研究的核心对象。
二、符号表示法及其发展
由于逻辑常项在逻辑研究中的核心地位,逻辑常项符号表示法的发展伴随着逻辑学发展的始终,并在根本上影响着逻辑学的最终样态。这是因为恰当的符号表示法可以方便我们以一种更加明晰的方式、更有效率地表达逻辑思想,并进而构建推理工具。
逻辑常项符号表示法的产生和发展我们可以将其归纳为三种形态:
第一种形态:自然语言表示法
逻辑常项的最初表达是使用自然语言表示的。
古希腊时期的亚里士多德在《前分析篇》中就使用如下语言表达常用的4种命题:
(1) A belongs to every B;
(2) A not belong to any B;
(3) A belongs to some B;
(4) A not belong to some B。
其中,大写字母A、B分别表示命题的主项和谓项,而“belongs to every”“not belong to any”“belongs to some”“not belong to some”则分别表示“都是”“都不是”“至少有些是”“并非都是”等4种逻辑常项。(参见张家龙,第318页;亚里士多德,第62页;cf.Barnes, 1995. p.4, 6, 24)
麦加拉-斯多葛学派深入地研究了命题逻辑,他们通过公理或推理规则研究了“否定”“不相容析取”“蕴涵”等的推理规律。他们对于逻辑常项同样是使用自然语言来表述的。如他们对“否定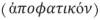 ”“合取
”“合取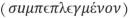 ”“析取
”“析取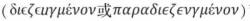 ”“蕴涵
”“蕴涵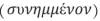 ”等分别用自然语言“并非
”等分别用自然语言“并非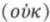 ”“并且
”“并且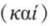 ”“或者
”“或者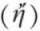 ”“如果
”“如果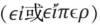 ”等来表述。(cf.Mates, pp.29-182)中世纪的逻辑教科书中,一般也使用符号“和(et)”“或(vel)”“如果(si)”等来表示合取、析取和条件关系。(cf. Bonevac and Dever, pp.175-233; De Rijk, pp.159-191)
”等来表述。(cf.Mates, pp.29-182)中世纪的逻辑教科书中,一般也使用符号“和(et)”“或(vel)”“如果(si)”等来表示合取、析取和条件关系。(cf. Bonevac and Dever, pp.175-233; De Rijk, pp.159-191)
中国先秦时期的墨家研究“名”“辞”“说”之辩学,他们对于逻辑常项也是使用自然语言来表达的。他们使用“或”来表示逻辑常项“部分是,但不全是”(“或也者,不尽也”),如《小取》中“马或白者,二马而或白也,非一马而或白”。(孙诒让,第421页)他们使用“且”表达通常的时态关系“即将”,如《小取》中“且斗鸡,非鸡也;……且入井,非入井也;止且入井,止入井也”。(同上,第419页)另外还有“假”等其他常项。
使用自然语言来表达逻辑常项,其最大优势是直观、容易理解。但是也存在缺陷,一是自然语言有歧义、含糊不清,二是作为研究对象的语言和用来研究的元语言混合在一起。
第二种形态:符号表示法
对于前述亚里士多德研究的四种命题,中世纪的威廉·谢尔沃德、奥赛尔的拉姆贝特和西班牙的彼得等人分别使用大写字母A、E、I、O来表示,这开辟了逻辑常项之符号表示的新纪元。之所以使用A、E、I、O来表达,一个原因是为了便于记忆,A、I分别是拉丁文单词“affirmo”(肯定)中的第一个和第二个元音字母,E、O分别是拉丁文单词“nego”(否定)中的第一个和第二个元音字母。(参见波波夫、斯佳日金,第212-213页)由此可见,A、E、I、O的使用虽然实现了逻辑常项由自然语言表示法到符号表示法的跨越,但是它在某种意义上实际是自然语言的一种简写,带有明显的由自然语言表示法到符号表示法的过渡痕迹。
逻辑常项符号表示法的使用使得逻辑常项的表示摆脱了自然语言的羁绊和束缚,其涵义更加明确、无歧义。
对逻辑常项符号表示法作出巨大贡献的应该是伟大的德国学者莱布尼兹。他提出了创建普遍语言和思维演算的构想,在此构想之下,莱布尼兹以符号“Non-A”“AB或A+B”“A∞B或A=B”等来表述“否定”“合取”“等值”等。(cf. Lenzen, pp.1-83)这开辟了使用符号来表示逻辑常项的新时代,这对后来逻辑学的发展产生了巨大的推动作用并影响深远直至今日。
十九世纪的逻辑学家皮尔士对逻辑常项的符号表示法做了大量的推进工作。他以不同类型的符号来表达涉及的个体变元、函数和关系等,他区分了相容析取和不相容析取,并分别以不同的逻辑符号“x+, y”“x+y”来表述之。(cf. Peirce, 2010, pp.317-378)他还以符号“∑”“∏”来表达存在量词和全称量词,使用∑ixi表示“xi+xj+xk+etc.”,使用∏ixi表示“xixjxk, etc.”。这些量词可以重叠使用,如∑i∏j∑k等。(cf. Peirce, 1996, pp.608-632)
德国逻辑学家弗雷格使用其独创的二维表意符号来表述逻辑常项。弗雷格区别观点的表述和对观点的断定,他使用二维横线表示内容短线,即以“——”表示内容短线,短线后是所表示的观点内容。二维符号:

表示表述观点A;二维符号:

表示断定观点A。增加的垂直竖线“|”称为断定短线。
在此基础上,他以内容短线下加上垂直竖线,表示否定。即以:

表示A的否定。以:
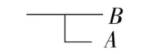
表示A蕴涵B。
通常的推理规则分离规则则表示为:由 和
和 ,可以得到:
,可以得到: 。
。
弗雷格还引入如下符号来表示全称量词: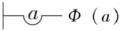 。
。
上述符号表示“对于任一个体a,函数Ф (a)都成立。”(Frege, pp.1-82)
弗雷格逻辑常项的二维表示法使得符号同时具有语法和语义的双重涵义,即弗雷格的符号表示法是一种形义兼具的表示法。(cf. ibid., pp.11-13)
一方面,弗雷格依据这一独特的符号表示法,构建了第一个现代谓项逻辑演算系统,开辟了逻辑学发展的新时代,这成为了现代逻辑诞生的标志性事件;另一方面,弗雷格的符号“虽然相当精确,但因为是二维的,因此很难掌握,也不便于应用,从历史上看,这就是造成弗雷格的《概念文字》在当时未能产生很大影响的重要原因之一”。(郑毓信,第52-53页)
意大利数学家皮阿诺给出了一套非常简洁的逻辑符号表示法:用符号“a∩b”“-a”“a∪b”“a⊃b”“a=b”来分别表示“合取”“否定”“析取”“蕴涵”和“等值”,使用符号“x,y,……”表示全称量词,符号“a⊃x,y,……b”就表示“对任意的x,y,……,都有a蕴涵b”。
皮阿诺创制的逻辑符号给罗素以极大启发,使得他将数学还原为逻辑的数学基础研究工作得以顺利进展。罗素和怀特海基于皮阿诺的符号系统创制了他们自己的逻辑符号系统。他们用符号“~p”“p∨q”分别表示“否定”“析取”,并以之作为初始联结词,定义引入其他联结词如“⊃”等。符号“p·q”“p⊃q”“p≡q”分别表示“合取”“蕴涵”和“等值”。在此基础上,他们以包含符号“p∨q”和“p⊃q”的公式,如“p∨p⊃p”“(q⊃r)⊃(p∨q⊃p∨r)”等作为公理,构建了命题逻辑的公理系统。他以符号“(x)”“(∃x)”分别表示“全称量词”和“存在量词”。(cf.Russell, 1967a, pp.124-125; Russell, 1967b, pp.150-182)其析取词符号“∨”和存在量词符号“∃x”直至今日仍然是被最广泛使用的逻辑常项符号。
尽管一阶谓词逻辑演算是由弗雷格首创的,但是真正引起人们广泛关注的是罗素和怀特海的《数学原理》,其中一个关键因素是罗素继承并进一步改进了皮亚诺的符号表示法体系。
数学家希尔伯特和阿克曼在《数理逻辑原理》中给出了与罗素系统稍有差别的符号表示法系统,其中至今被广泛使用的差别之一是以“X→Y”取代“p⊃q”。《数理逻辑原理》与其符号表示法相关的是对命题逻辑、一阶谓词逻辑和二阶谓词逻辑进行了区分,并分别给出了相应系统的逻辑符号体系。(cf. Hilbert and Ackermann)
第三种形态:形式化表示法
当符号表示法中的符号不再仅仅表达某一个确定的逻辑常项,符号的涵义仅仅由表达它的公式或者规则来唯一规定时,这时的符号表示法就实现了向形式化表示法的华丽转身。
英国数学家、逻辑学家布尔创立了布尔代数。其中含有3个逻辑常项符号:“×”“+”“-”,这些符号的意义仅仅由表达它的公式决定:(1)X+Y=Y+X,X×Y=Y×X;(2)X×(Y+Z)=(X×Y)+(X×Z),X+(Y×Z)=(X+Y)×(X+Z);(3)X+0=X,X×1=X;(4)X+(-X)=1,X×(-X)=0。这些常项并不表示某一个确定的涵义,只要对这些常项所给的解释符合上述公式的规定,都可以作为这些常项的解释。例如,可以将“×”“+”“-”解释为集合论中的“交”“并”“补”运算,也可以将“×”“+”“-”解释为开关电路中的“串联”“并联”“开关”运算,还可以将“×”“+”“-”解释为逻辑运算中的“合取”“析取”“否定”。布尔代数中的常项符号表示法就属于形式化表示法。
现代逻辑各种形式系统中,所采取的基本都是语法和语义相分离的构建模式。在这些形式系统中,逻辑常项的意义唯一地由表达它的公理和变形规则决定。例如,同样是符号“┐”和“→”,在经典命题逻辑中,其意义由公理“(┐A→B)→((┐A→┐B)→A)”等和规则“若A且A→B,则B”决定;而在直觉主义命题逻辑中,其意义则由公理“┐A→(A→B)”等和规则“若A且A→B,则B”决定。再如,对于模态联接词符号“□”在K、D、T、S4、S5等不同的系统中,由于表达“□”的公理不尽相同,其所表达的也是不同意义的“必然”。
综观逻辑常项符号表示法的产生和发展历程,可以看出:历史上的逻辑符号表示法经历了由自然语言表示法到人工语言表示法的发展历程。人工语言表示法又经历了人工表意符号语言和形式化语言两个阶段。在世界三大逻辑发源地的早期逻辑研究中,都比较普遍地使用自然语言来研究推理关系。并且在古代中国的名辩研究、印度的因明研究中,这种传统一直在保持着;只有在西方,逻辑表示法经历了由自然语言到人工语言的嬗变,并进一步发展到形式化语言的新阶段,也正是在西方,逻辑学获得了持续而深入的不断发展,并进而诞生了现代逻辑。即使同样是人工语言,相较于一般的符号表示法,形式化表示法推动逻辑学研究实现了由基于推理实际的具体思维规律的描述性研究到基于结构变换的纯粹推理模式的规范性研究的转变。这种转变从根本上改变了逻辑的样貌,拓展了逻辑研究的广度和深度。
由此可见,逻辑常项表示法的变迁,不仅决定着逻辑形态的呈现形式,而且决定着逻辑研究的持续和深入发展。对此,著名逻辑学家皮亚诺非常明确地指出,有些研究之所以还没有满意的结果,其“困难的根源是语言含混。”他认为,符号语言对于剖析出算术和几何的原理,以及辨别其初始的和从属的概念、定义、公理和定理等等都是不可少的工具,同时也是陈述那些日常语言几乎不能表述的复杂思维过程的手段。(参见王宪钧,第299页)19世纪末至今现代逻辑的发展也充分地证明了这一点。
三、括号表示法
当下,国际通行的逻辑常项表示法主要有两种,即皮阿诺、罗素等人创制的中置表示法(简称中置法)和波兰逻辑学家卢卡西维茨等人发明的前置表示法(简称前置法)。其中,前置法又称波兰表示法,简称波兰记法。与波兰记法相类的还有后置法,其与前置法的差异只是顺序相反。
与这两种表示法不同,下面我们将阐述一种新的逻辑常项符号表示法——括号表示法。
括号表示法是一种仅使用一对括号来表达所有逻辑常项的符号表示法。将完全纯粹的括号表示法作为一种独立的逻辑常项表示法是作者于2019年提出的。(参见杜国平,2019年a,第7-12页)
(一)括号表示法的源起
括号表示法的明确提出是受到舍弗(H. M. Sheffer)函数和张清宇先生相关工作的启发。
舍弗函数将所有的命题联接词归约为一个逻辑函数,即析舍或者合舍,通常用符号“|”“↓”表示。析舍和合舍的表达能力都很强,可以表达所有的命题联接词。受此启发,我们考虑是否可以创制表达能力更强的逻辑常项,不仅能表达所有的命题联接词,而且能同时将其他逻辑常项如量词、模态词等进行进一步归约为一个逻辑常项。
张清宇先生在1995年提出:“常见的经典命题逻辑系统中总是联结词和括号兼而有之,也就是说构造合式公式时所要求于它们的联结作用和分组作用分别由两类符号承担。实际上,这两种作用在经典命题逻辑系统中是可以由一类符号来承担的。”基于此,他构建了只含有命题变项、命题常项“t”和左右括号“( )”的命题逻辑形式语言及其公理系统。在该文中,张清宇先生给出的括号“(AB)”相当于二元联结词“A^┐B”,“t”相当于零元联接词“1”。(参见张清宇,1995年,第40-47页)
1996年,张清宇先生又进一步构建了不用通常的命题联结词和量词的一阶逻辑系统。在该文中括号“(AB)”相当于二元联结词“A^┐B”;附加变元的括号“(AxB)”相当于联结词“∃x\[A^┐B\]”。(张清宇,1996年,第72-79页)在该系统中,括号表示两个不同的逻辑常项,其中同样带有零元联接词“T”。在该系统中,存在三个逻辑常项:零元联接词“T”、二元联接词“(AB)”和量词“(AxB)”。
在张清宇先生上述工作的基础上,本文作者经过数年研究于2019年提出了不再使用零元联结词而纯粹使用括号来表示所有逻辑常项的基本想法,并正式提出括号表示法;(参见杜国平,2019年b,第56-60页)于2020年将括号表示法由二值命题逻辑和一阶量词逻辑推广到多值逻辑系统之中;(参见杜国平,2020年,第36-49页)于2021年提出将括号表示法推广到任一逻辑系统之中,并且完成了最为关键的一步:证明了仅仅使用一对括号就可以表达任一逻辑系统内所有的逻辑常项,正式确立了作为一种独立的逻辑常项符号表示法的括号表示法。
括号表示法不同于中置法和前置法,它是由中国学者提出的一种新的逻辑常项表示法;前置法由波兰学者提出,也称波兰表示法,因此也可以将括号表示法称为中国表示法。
(二)何谓括号表示法
下面我们以一阶模态谓词逻辑为例来阐明括号表示法的基本思想。
在一阶模态谓词逻辑的形式语言LP中,其他符号均与通常的系统相同,只是其中的命题联接词、量词和模态词等逻辑常项只使用一个符号,即一对左右括号“(”“)”。
与通常的合式公式形成规则类似,涉及“( )”的公式递归定义如下:
定义3.01 若A、B、C、D、E是公式, x是不在A、B、C中出现的自由变元,则(ABCDxE)亦是公式。
在形式语言LP中,只有一个逻辑常项,即仅仅使用括号的五元组“(ABCDxE)”。
形式语言LP中所有公式的集合记为Form(LP)。
使用克里普克的可能世界语义,公式(ABCDxE)的语义规定为:
定义3.02 设<M,W,R,H,V>是任一五元组,其中M、W是两不相交的非空集,M是个体集,W是世界集,R是W上的二元关系,H是W到M的幂集上的映射。对于任意可能世界w、w′∈W,一个赋值V是Form(LP)与W的笛卡尔积到集合{1, 0}上的映射,即:
V:Form(LP)×W→{1,0}
除满足通常的条件之外,还满足:
V((ABCDxE), w)=1当且仅当V(A, w)=0或者V(B, w)=0;并且对于任一w′,若Rww′,则V(B, w′)=0或者V(C, w′)=1;并且对于任何m∈M,任一w∈W,都有V(u/m)(D(u), w)=0或者V(u/m)(E(u), w)=1。(参见周北海,第344-382页)
在形式语言LP中,通常的命题联接词、全称量词和必然模态词是通过如下一组定义仅仅借助唯一的逻辑常项符号“( )”而引入的:
定义3.03
(A) =def (AAAAxA)
[AB] =def (ABBBxB)
【C】=def (C(C)CCxC)
「Dx」 =def (C(C)(C)(D)xD)
根据定义3.02,可以得出上述引入逻辑常项的语义:
定理3.01 设<M,W,R,H,V>是任一五元组,其中M、W是两不相交的非空集,M是个体集,W是世界集,R是W上的二元关系,H是W到M的幂集上的映射。对于任意可能世界w、w′∈W,一个赋值V是Form(LP)与W的笛卡尔积到集合{1, 0}上的映射,则有:
(1)V((A), w)=1,当且仅当V((AAAAxA), w)=1,当且仅当V(A, w)=0或者V(A, w)=0;并且对于任一w′,若Rww′,则V(A, w′)=0或者V(A, w′)=1;并且对于任何m∈M,任一w∈W,都有V(u/m)(A(u), w)=0或者V(u/m)(A(u), w)=1,当且仅当V(A, w)=0。
(2)V([AB], w)=1,当且仅当V((ABBBxB), w)=1,当且仅当V(A, w)=0或者V(B, w)=0;并且对于任一w′,若Rww′,则V(B, w′)=0或者V(B, w′)=1;并且对于任何m∈M,任一w∈W,都有V(u/m)(B(u), w)=0或者V(u/m)(B(u), w)=1,当且仅当V(A, w)=0或者V(B, w)=0。
(3)V(【C】, w)=1,当且仅当V((C(C)CCxC), w)=1,当且仅当V(C, w)=0或者V((C), w)=0;并且对于任一w′,若Rww′,则V((C), w′)=0或者V(C, w′)=1;并且对于任何m∈M,任一w∈W,都有V(u/m)(C(u), w)=0或者V(u/m)(C(u), w)=1,当且仅当V(C, w)=0或者V(C, w)=1;并且对于任一w′,若Rww′,则V(C, w′)=1或者V(C, w′)=1;并且对于任何m∈M,任一w∈W,都有V(u/m)(C(u), w)=0或者V(u/m)(C(u), w)=1,当且仅当对于任一w′,若Rww′,则V(C, w′)=1。
(4)V(「Dx」, w)=1,当且仅当V((C(C)(C)(D)xD)=1,当且仅当V(C, w)=0或者V((C), w)=0;并且对于任一w′,若Rww′,则V((C), w′)=0或者V((C), w′)=1;并且对于任何m∈M,任一w∈W,都有V(u/m)((D)(u), w)=0或者V(u/m)(D(u), w)=1,当且仅当V(C, w)=0或者V(C, w)=1;并且对于任一w′,若Rww′,则V(C, w′)=1或者V(C, w′)=0;并且对于任何m∈M,任一w∈W,都有V(u/m)(D(u), w)=1或者V(u/m)(D(u), w)=1,当且仅当对于任何m∈M,都有V(u/m)(D(u), w)=1。
通过定理3.01可以看出,(A)、[AB]、【C】和「D」分别表达了否定、析舍、必然模态和全称量词等逻辑常项的语义。即5元组(ABCDxE)仅仅使用一对括号就同时表达了否定、析舍、必然模态和全称量词等逻辑常项。
从语法的角度看,使用通常的符号表示法(ABCDxE)实际上表达着如下一个复杂的5元逻辑常项:
(ABCDxE) ≡ {┐A∨┐B}^□{B→C}^∀x{Dx→Ex}
由此可以得出:
(A)≡(AAAAxA)≡┐A
[AB]≡(ABBBxB)≡┐A∨┐B
【C】≡(C(C)CCxC)≡□C
「Dx」≡(C(C)(C)(D)xD)≡∀xDx
由此可以更加清晰地看出,仅仅使用一对括号,5元组(ABCDxE)是如何能够同时表达否定、析舍、必然模态和全称量词等逻辑常项的。
进一步可知,若定义<AB>=def[A(B)],则<AB>≡[A(B)]≡A→B。
因此,对于通常的逻辑公理和推理规则(对于由这些公理和推理规则构成的系统记为PQNK系统)使用括号表示法可以分别表示为:
Ax1 <B<CB>>
Ax2 <<B<CD>><<BC><BD>>>
Ax3 <<(B)C><<(B)(C)>B>>
Ax4 <「<BCx>」<B「Cx」>>,x不在B中出现
Ax5 <「Bx」Bt>,Bt是由将Bx中的x全部替换为t而得
K公理 <【<BC>】<【B】【C】>>
分离规则 若B,且<BC>,则C。
量化规则 若Bu,则「Bx」。
必然化规则 若B,则【B】。
根据定义3.03等可知,这些公理中的逻辑常项都仅仅是使用一对括号“(”“)”由同一个逻辑常项来表达的。
(三)括号表示法的结构特征
假设在形式语言LP*中,其他非逻辑常项符号与通常的形式语言相同,而逻辑常项符号只有仅仅使用一对左右圆括号的n元联接词(C1C2……Cn-1Cn)。下面我们来讨论其若干结构特征。
我们使用大写字母X、Y、Z及其加下标的形式来表示任一表达式。LP*中所有表达式的集合记为Expr(LP*)。由LP*中所有原子公式构成的集合记为Atom(LP*),由LP*中所有公式构成的集合记为Form(LP*)。
定义3.04 Form(LP*)是满足以下(1)-(2)的表达式集合S中的最小集:
(1)Atom(LP*)⊆S;
(2)若X1,X2,……,Xn-1,Xn∈S,则(X1X2……Xn-1Xn)∈S。
通常用字母A、B、C、D(或加下标)等表示任一LP*的公式;用∑、Γ、Δ等表示任一LP*的公式集合。
定理3.02 设R是关于表达式的一个性质。若:
(1) 对于任一公式A∈Atom(LP*),均有R(A);
(2) 对于任一公式C1, C2,……,Cn-1,Cn∈Form(LP*),若R(C1), R(C2),……, R(Cn-1), R(Cn),则R((C1C2……Cn-1Cn))。
那么对于任一公式A∈Form(LP*),都有R(A)。
定义3.05 一个由形式语言LP*中符号构成的任一有穷序列称为一个表达式;一个表达式中出现的符号数目,称为表达式的长度。
定义3.06 两个表达式X和Y是相等的,当且仅当它们长度相同,且依次出现的符号均相同。记为X=Y。
定义3.06 设X、Y、Z1和Z2是任意表达式,如果X=Z1YZ2,则称Y为X的段。如果Y是X的段,且X≠Y,则称Y是X的真段。
定义3.07 设X、Y、Z是任意表达式,如果X=YZ,则称Y为X的初始段,Z为X的结尾段。如果Z不空,则称Y为X的真初始段;如果Y不空,则称Z为X的真结尾段。
定理3.03 形式语言LP*中的任一公式都是不空的表达式。
定理3.04 形式语言LP*中的任一非原子公式均以括号开头,以括号结尾。
定理3.05 形式语言LP*中任一公式及其任一不空的真初始段中,左括号的出现比右括号多;形式语言LP*中任一公式及其任一不空的真结尾段中,右括号的出现比左括号多。
根据定理3.04和3.05可知:
定理3.06 形式语言LP*中的任一公式的真初始段和真结尾段都不是LP*的公式。
定理3.07 形式语言LP*中的任一公式仅有两种形式之一:原子公式或者形如(C1C2……Cn-1Cn)的公式;并且在各种情形下公式所具有的形式是唯一的。
定义3.08对于公式(C1C2……Cn-1Cn),称Ci(1≤i≤n)为公式(C1C2……Cn-1Cn)的第i项。
定义3.09假设C1, C2,……, Cn-1, Cn∈Form(LP*)。若(C1C2……Cn-1Cn)为公式C的构成部分,则称公式C1, C2,……, Cn-1, Cn为(C1C2……Cn-1Cn)最外层的一对括号( )在C中的辖域,称Ci(1≤i≤n)为(C1C2……Cn-1Cn)最外层的一对括号( )所辖的第i项。
定理3.08假设C1, C2,……, Cn-1, Cn∈Form(LP*)。若(C1C2……Cn-1Cn)为公式C的构成部分,则对于(C1C2……Cn-1Cn)最外层的一对括号( )在C中有唯一所辖的第i项Ci(1≤i≤n)。
证明:施归于(C1C2……Cn-1Cn)中所辖项的次序。
当i=1时,即对于(C1C2……Cn-1Cn)中所辖的第1项,假设(C1C2……Cn-1Cn)最外层的一对括号( )在C中所辖的第1项不是唯一的,则至少存在C11和C12均是(C1C2……Cn-1Cn)最外层的一对括号( )在C中所辖的第i项,且C11≠C12。
一方面,根据定义3.04公式的定义规则可知,C11和C12都是形式语言LP*中的公式。
另一方面,因为C11和C12均是(C1C2……Cn-1Cn)最外层的一对括号( )在C中所辖的第1项,则左括号“(”是C中的同一个符号,所以C11、C12均以C中“(”之后的同一个符号开始,因此根据定义3.07可知,或者C11是C12的真初始段,或者C12是C11的真初始段。根据定理3.06可知,或者C11不是形式语言LP*中的公式,或者C12不是形式语言LP*中的公式。
两相矛盾,假设不成立。
因此,对于(C1C2……Cn-1Cn)最外层的一对括号( )在C中有唯一所辖的第1项C1。
假设原命题对于所辖项的次序小于等于i-1均成立,当所辖项的次序为i时,假设(C1C2……Cn-1Cn)最外层的一对括号( )在C中所辖的第i项不是唯一的,则至少存在Ci1和Ci2均是(C1C2……Cn-1Cn)最外层的一对括号( )在C中所辖的第i项,且Ci1≠Ci2。
一方面,根据定义3.04公式的定义规则可知,Ci1和Ci2都是形式语言LP*中的公式。
另一方面,因为Ci1和Ci2均是(C1C2……Cn-1Cn)最外层的一对括号( )在C中所辖的第i项,则左括号“(”是C中的同一个符号,并且其后所辖的第i-1项均相同,所以Ci1、Ci2均以C中“Ci-1”之后的同一个符号开始,因此根据定义3.07可知,或者Ci1是Ci2的真初始段,或者Ci2是Ci1的真初始段。根据定理3.06可知,或者Ci1不是形式语言LP*中的公式,或者Ci2不是形式语言LP*中的公式。
两相矛盾,假设不成立。
因此,对于(C1C2……Cn-1Cn)最外层的一对括号( )在C中有唯一所辖的第i项Ci。
所以,定理成立。
这说明括号表示法的语言是无歧义的,其公式结构具有唯一性、精确性。(杜国平,2019年b,第35-41页)
(四)与其他两种表示法的比较
中置法将二元逻辑常项置于所联结的两个命题项的中间,如表示蕴涵、合取、析取、等值等的公式“C→D”“C^D”“C∨D”“C↔D”。这符合人们通常对二元运算的使用直觉,因为算术中通常使用的如“+”“-”“×”“÷”等二元运算,也是将其置于两个数的中间。但是在遇到比较复杂的公式时,二元逻辑常项的辖域可能造成误解,中置法需要借助其他辅组符号如括号等来表示结合的先后顺序,以排除其可能造成的歧义性。
波兰表示法将逻辑常项置于所联结命题项前面,其具体做法是分别使用“Np”“Cpq”“Kpq”“Apq”“Epq”等来表示“否定”“蕴涵”“合取”“析取”“等值”。(£ukasiewicz, pp.22-30)使用符号“Π”来表示全称量词。特别值得一提的是,波兰表示法还使用变量函子“φ(p)”来表示“φ是任一作用于p之上的一元联结词。”这样符号“ΠpΠqCEpqCφpφq”就表示“对于任一命题p和q,如果p和q等值,那么φ(p)蕴涵φ(q)”,其中 “φ”可以是“任一关于p的一元真值函数”。(cf.£ukasiewicz, pp. 92-102)波兰记法中逻辑常项的辖域是唯一确定的,因此它不需要使用括号等符号来表示结合的先后次序。但是这种记法的优点却背离了自然语言中所使用的构造方式,因此在读法上十分困难。(参见威廉·涅尔、玛莎·涅尔,第652页)
括号表示法与波兰表示法相对,对于逻辑常项的表示仅仅使用括号而不使用通常的联接词、量词和模态词等。因为括号表示法只使用括号,而不再使用其他逻辑常项符号,所以,若以一对括号作为一个逻辑常项表示单位,那么运用括号表示法表达的公式,其长度比中置法简短。例如对于常见的经典命题逻辑公理系统的两条正命题公理,在括号表示法中,如前所述可以简单而直接地表示为:
Ax1 <B<CB>>
Ax2 <<B<CD>><<BC><BD>>
其中仅仅含有一种括号,而不再需要其他联接词符号。
括号表示法是左右成对使用,其辖域及其所辖顺序各项非常清晰,所以,它比波兰表示法清晰。(参见杜国平,2019年c,第21-24页)
中置法对括号的归约能力主要体现在舍弗(H. M. Sheffer)函数,但是未出现对命题逻辑词、量词和模态词等逻辑常项的统一归约;理论上讲,波兰表示法可以对各种逻辑常项进行归约,但是遗憾的是历史上亦未曾出现,实际上波兰表示法即使使用一个符号对各种逻辑常项进行归约,但是因为其没有括号,虽然不会导致歧义,但是辖域的识别亦是非常困难的。另外,若使用波兰表示法对各种逻辑常项进行归约,必须注明其元数,否则辖域不清楚;而括号表示法的辖域就是左右两个括号中间的项,辖域清晰。
括号表示法可以对所有的逻辑常项进行归约,前述已经证明了这一点,这显示出括号表示法强大的功能,某种意义上是最大的表达功能,因为它只有一对左右括号。括号表示法之所以表达能力强于其他表示法,主要是因为:在一个逻辑表达式中,需要两类符号,一类是逻辑常项符号,一类是区分结合先后顺序或层次的符号。在中置法中,前一类符号是使用“┐”“^”“→”等符号来表达的,后一类符号是使用括号来表达的;在波兰表示法中,因为前置法中的每一个逻辑常项的元数和结合次序(从左往右)是唯一确定的,因此,其逻辑常项同时发挥着第二类符号的功能,因此前置法不需要括号,只有一类符号就足够了。而括号表示法既发挥了括号的第二类符号功能,同时使其兼具逻辑常项的功能,因此只有一类符号就足够了。另外因为括号内符号的元数不受限制,所以括号表示法可以通过增加元数而不断增强其表达功能,这是波兰表示法难以实现的,因为目前波兰表示法中的每个逻辑常项其元数是固定的,这就限制了其对逻辑常项的归约能力。
与其他逻辑符号表示法相比,括号表示法在使用上还具有如下特点或优势:
1.直观,更易接受。括号本身就有确定先后顺序的结构功能,括号表示法充分利用这一点,并在此基础上再赋予括号以逻辑函数功能,便于学习,容易形成代入感,而不会像特设的、专门的人造符号那样让初学者望而生畏,并需要死记硬背。(参见杜国平,2021年a,第52-56、78页)
2.更加自然。常用的逻辑符号“┐”“^”“∨”“→”“↔”等是人为定制的,与之相比,括号是常用书面语言中本身就有的,人们使用起来比较习惯。
3.更加方便,便于录入。括号在人们使用的语言中更常用,不同的自然语言、不同的专业学科语言中基本上都使用括号。
4.灵活。作为形式语言符号的括号既可以表示一元联结词(A),也可以表示二元联结词(AB)、三元联结词(ABC)、四元联结词(ABCD)、……,它可以表示任意n元命题联结词;还可以直接使用惯常的记法表示量词(x)A(x)、各类模态词[A]、【B】等,表达非常灵活。其意义仅由表达它的语法公理或者语义定义而确定。(参见杜国平,2021年b,第53-61页)
5.描述能力强。通过引入不同括号如“( )”“[]”“<>”“【】”“〈〉”“{}”“「」”“『』”“〖〗”“(())”等来表示不同元数的不同连接词,还可以进一步增强括号表示法的描述能力。为了增加可识别性,还可以约定以单线括号如“( )”“[]”等表示一元联结词,以双线括号如“〖〗”“(())”等表示二元联结词,以粗线括号如“【】”“ ”等表示模态词等。
”等表示模态词等。
6.整体性。其作用的对象被包括在一对括号之内,辖域非常清晰。
中置法和波兰表示法都是分离表示法。括号表示法与之不同,它是一种整体表示法,在设计思想上是一种完全不同的符号表示法。之所以称其他两种符号表示法为分离表示法,是因为中置法将运算符号或联接词左右的两个符号断开,当其作为一个单元形成更复杂的公式时(如p∨q→r),需要括号或者其他规定来确定运算的先后顺序;波兰表示法虽然运算顺序是明确的,但是因为相互临近的两个符号是分置的,当公式足够复杂时(如CKCNpCpqrs),确立运算顺序也非易事。反之,括号表示法中因为括号是两个成对同时使用的,并且它将所作用的其他符号包含其中,使其和作用的符号作为一个整体连接在一起,辖域清楚,并且结合顺序和运算顺序非常明确。(参见杜国平,2020年,第36-49、167页)
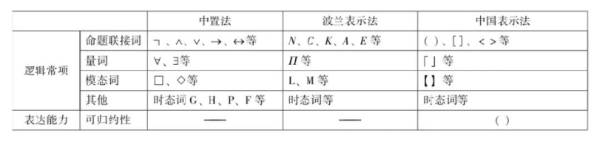
三种表示法的基本情况对照如下:
四、余论
基于易辨识、可读性等方面的要求,括号表示法还可以添加一些辅助性的修饰,使其表达更加清晰明白。
一种办法是括号的加标表示法。如(nDn)以左括号加数字上标表示逻辑常项辖域的左起,以右括号加相同数字下标表示逻辑常项的右起;不同数字的上下标表示若干不同的逻辑常项或处于不同位置的逻辑常项。
加标括号表示法甚至可以不用括号(此时可以直接称其为加标表示法),直接用加不同数字的上下标来表达各种逻辑常项
在实际运用中,可将不同符号表示法的优点结合起来使用。例如,因为一元联接词的辖域清晰,可保留中置法中已经习惯的常用符号如否定符“┐”等;而其他多元逻辑常项,则可使用括号表示法中的符号,以发挥其辖域清晰、表达简练的特点。
犹如天文学家借助于各种望远镜观察宇宙,生物学家利用显微镜观察生物结构,逻辑学家则借助符号语言进行纯粹形式的思想创新。形式语言是现代逻辑学家研究推理问题不可或缺的工具,而逻辑常项是形式语言的核心表达要素之一,恰当的逻辑常项表示法可以为逻辑研究提供更加适用、更加高效的研究工具。不仅如此,从某种意义上说,各种不同的逻辑系统实际上是关于不同逻辑常项的逻辑,逻辑发展史也可以看做逻辑常项的研究史。因此,逻辑常项的符号表示法也应该成为逻辑研究的核心内容之一。
逻辑学的创新发展离不开逻辑符号表示法的不断创新,但是长期以来,关于逻辑符号表示法的研究相对缺乏,尤其是系统性的历史考察和总结尚没有得到学界的高度重视,相关研究亟待加强。
现代理论和技术的进步为逻辑符号表示法的进步提供了更加广阔的发展空间,但是近百余年来,逻辑符号表示法鲜有进步和创新。逻辑符号表示法可以充分利用当代科技发展的有利条件,尝试探索更加适用的符号表示方法。例如,对于模态逻辑中的模态算子□、◇,至少可以尝试以下几种表示法:
(1) 以线条的粗细来识别不同的模态:将线条加粗以AB来表达必然命题□(AB),以(AB)来表达实然命题(AB),将线条虚化以AB来表达可能命题◇(AB)。
(2) 以线条的颜色来识别不同的模态。
(3) 以线条的背景来识别不同的模态。
以此来表示推理关系,或许更加生动。
在此基础上,进一步深入研究相关表示法的特点,以利于推理理论以及相关理论的创新研究和应用研究。例如,上述方法至少在可视化、机器识别等方面有其独特的应用价值。
逻辑学本是非常抽象的学问,但是利用现代技术,完全可以对其符号表示法进行创新,使得理性思考不再永远板着面孔。理性思考完全可以做到既抽象纯粹,又形象灵动!
【参考文献】
[1] 波波夫、斯佳日金,1984年:《逻辑思想发展史》,上海译文出版社。
[2]杜国平,2019年a:《关于“不用联结词的逻辑系统”的注记》,载《重庆理工大学学报(社会科学)》第4期。
2019年b:《基于括号表示法的一阶逻辑系统》,载《安徽大学学报(哲学社会科学版)》第3期。
2019年c:《不用联结词的“舍……取……”型自然推演系统》,载《湖南科技大学学报(社会科学版)》第3期。
2020年:《基于括号表示法的4值逻辑自然演绎系統》,载《湖北大学学报(哲学社会科学版)》第2期。
2021年a:《“不可得兼”型命题逻辑自然推演系统》,载《广西大学学报(哲学社会科学版)》第3期。
2021年b:《合舍系统及其定理的能行证明》,载《重庆理工大学学报(社会科学)》第6期。
[3]孙诒让,2017年:《墨子间诂》,中华书局。
[4]王宪钧,1982年:《数理逻辑引论》,北京大学出版社。
[5]威廉·涅尔、玛莎·涅尔,1985年:《逻辑学的发展》,张家龙、洪汉鼎译,商务印书馆。
[6]亚里士多德,2018年:《工具论》,刘叶涛等译,上海人民出版社。
[7]张家龙,2004年:《逻辑学思想史》,湖南教育出版社。
[8]张清宇,1995年:《不用联结词的经典命题逻辑系统》,载《哲学研究》第5期。
1996年:《不用联结词和量词的一阶逻辑系统》,载《哲学研究》第5期。
[9]郑毓信,1989年:《现代逻辑的发展》,辽宁教育出版社。
[10]周北海,1997年:《模态逻辑导论》,北京大学出版社。
[11]Barnes, J., 1995, The Complete Works of Aristotle, Volume 1: The Revised Oxford Translation, Princeton: Princeton University Press.
[12]Bonevac, D. and Dever, J., 2012, “A History of The Connectives”, in Dov M. Gabbay, F. J. Pelletier and J. Woods (eds.), Handbook of the History of Logic, Volume 11: Logic: A History of Its Central Concepts, Amsterdam: Elsevier.
[13]De Rijk, L. M., 1967, Logica Modernorum: A Contribution to The History of Early Terminist Logic, Vol. II Part Two, Texts, Indices, Assen: Van Gorcum.
[14]Elliott, M., 2015, Introduction to Mathematical Logic (6th ed.), Boca Raton, Florida: CRC Press.
[15]Frege, G., 1967 “Begriffsschrift, a Formula Language, Modeled upon that of Arithmetic, for Pure Thought”,in J. Van Heijenoort (ed.), From Frege to Gödel: A Source Book in Mathematical Logic, 1879-1931, Cambridge: Harvard University Press.
[16]Hilbert, D and Ackermann, W., 1950, Principles of Mathematical Logic, R. E. Luce (ed.), New York: Chelsea Publishing Company.
[17]Lenzen, W., 2004, “Leibniz's Logic”, in Dov M. Gabbay and J. Woods (eds.), Handbook of the History of Logic, Volume 3: The Rise of Modern Logic: from Leibniz to Frege, Amsterdam: Elsevier.
[18]£ukasiewicz, J., 1966, Elements of Mathematical Logic, Oxford: Pergamon Press.
[19]Mates, B., 1961, Stoic Logic, Berkeley, CA: University of California Press.
[20]Peano, G., 1967, “The Principles of Arithmetic, Presented by a New Method”, in J. Van Heijenoort (ed.), Frege to Gödel: A Source Book in Mathematical Logic,1879-1931, Cambridge: Harvard University Press.
[21]Peirce, C. S., 1996, “On the Algebra of Logic: A Contribution to the Philosophy of Notation”, in W. Ewald (ed.), From Kant to Hilbert Volume 1: A Source Book in the Foundations of Mathematics, Oxford: Oxford University Press.
2010, “Description of a Notation for the Logic of Relatives, Resulting from an Amplification of the Conceptions of Boole's Calculus of Logic”, in Memoirs of the American Academy of Arts and Sciences, New Series 9(2).
[22]Russell, B., 1967a, “Letter to Frege”, in J. Van Heijenoort (ed.), From Frege to Gödel: A Source Book in Mathematical Logic,1879-1931, Cambridge: Harvard University Press.
1967b, “Mathematical Logic as Based on the Theory of Types”, in J. Van Heijenoort (ed.), From Frege to Gödel: A Source Book in Mathematical Logic, 1879-1931, Cambridge: Harvard University Press.
















 潘梓年
潘梓年 金岳霖
金岳霖 贺麟
贺麟 杜任之
杜任之 容肇祖
容肇祖 沈有鼎
沈有鼎 巫白慧
巫白慧 杨一之
杨一之 徐崇温
徐崇温 陈筠泉
陈筠泉 姚介厚
姚介厚 李景源
李景源 赵汀阳
赵汀阳













