摘要:波普尔的概率解释工作主要包括批判主观解释和修正客观解释，这两个方面都与量子力学解释密不可分。早期波普尔就曾利用频率解释化解量子不确定性问题，解释量子干涉现象更是他后来由频率解释转向倾向性解释的重要动机。波普尔一直认为概率问题是量子力学解释的核心，而量子疑难几乎都是因为主观解释的入侵导致的。可是他的倾向性量子力学解释却遭到了很多学者的反驳，主要问题在于量子概率的高度非经典性。事实上，波普尔在对量子逻辑的反驳中犯的错误充分暴露了经典概率演算与量子力学的数学结构之间的冲突。应该说，波普尔对量子力学正统解释的反思是值得重视的，尽管他与其他人一样未能成功地兼顾所有的量子疑难。我们应当从波普尔的一系列研究中看到各个领域之间的内在关联，并充分认识量子力学解释问题的复杂性和独特性。

关键词:波普尔 概率解释 量子力学解释 频率解释 倾向性解释

概率哲学在波普尔的思想体系中无疑占据着至关重要的位置，他在《科学发现的逻辑》中用了超过一半的篇幅来讨论概率问题①,并在其整个学术生涯中反复提醒人们注意相关的论证。在波普尔的量子力学解释理论中，他的概率解释也起着决定性的作用。他的客观主义概率解释经历了从频率解释到倾向性解释的转变，这个过程既受到了量子力学解释的影响，又反过来影响了他的量子力学解释，后者体现在从早期以频率解释为核心的量子力学解释向后期的量子力学倾向性解释的演化中。相应地，波普尔量子力学解释的困难也与他的概率解释紧密相关，正如本文第五节将要论证的，这种困难集中体现在他反驳量子逻辑时所犯的错误之中。考虑到量子逻辑对量子力学解释的意义，波普尔对量子逻辑的反驳也映射了他的量子力学解释与“量子逻辑解释”之间的冲突，这种冲突当然也渗透着他对概率的理解。

波普尔的量子力学和量子逻辑思想与概率解释的相互影响和渗透既揭示了物理学、概率哲学和逻辑学之间的紧密联系，又反映出经典物理学、经典概率演算与量子力学数学结构的冲突。对波普尔的概率解释和量子力学解释的研究有助于深刻认识量子力学基础与经典的概率、逻辑观念进行调和时所遭遇的困难。这种认识是不断深化量子力学基础问题研究的必要条件。

一、反对主观解释(1)

出于确认度(degree of corroboration)理论的需要，波普尔把条件概率视作最基本的概率表达式，p(a,b)表示a在b的条件下发生的概率。(2)他把概率解释分成主观解释和客观解释两类。主观解释通常把概率解释为确定或相信的程度。在这里，逻辑解释被波普尔归为主观解释的一个变种；它把概率看成两个陈述之间的一种逻辑关系，p(a,b)就是陈述a能够从陈述b推导出来的程度。与主观解释相反，客观解释用独立于主观信念的方式解释概率。频率解释就是一种重要的客观解释，它把p(a,b)解释成在b的条件下形成的无限序列中a出现的频率。③

波普尔从一开始就站在客观解释这边，立场鲜明地反对主观解释。他指出两种概率解释有一个重要区别。对于客观解释，b表示可重复的实验条件；任意两次实验之间必须是相互独立的。否则，若这一次的实验结果取决于上一次实验的结果，那么这两次实验只能算是同一个实验的两个步骤，而不是同一个实验重复了两次。(3)然而在主观解释中，b必须囊括一切背景知识，包括先前的实验结果，因此总会受到这些实验的影响，是不断变动的，而且是我们无法选择的。对于客观解释，b是根据情况选取的，因此我们可以通过实验设置的选择来修改b,进而观察相应的概率的变化。⑤波普尔认为这个区别揭示了主观解释的致命缺陷，这可以总结为以下四点。第一，概率演算系统必然要求每一次实验的独立性，否则人们就可以构造稳赢的赌博机制(也称“大弃赌”或“荷兰赌”)⑥;因此即便我们承认先前的实验结果c应当被加入到b中，根据独立性所得的概率演算结果p(a,bc)=p(a,b)也要求我们忽略c。第二，概率论中的一些重要定律(例如关于独立试验的概率计算公式和大数定律)都以实验的独立性为前提；如果b是不断变动的，那么这些定律就都失效了，主观主义者对它们的运用就都不合法。⑦第三，主观解释把b看作我们的全部知识，因此也必定认为它是不断增长的，p(a,b)自然也会随之变化。主观主义者希望p(a,b)趋近于某个真实的、客观的概率值，然而这正是客观解释的主张。(4)第四，如果我们像主观主义者所主张的那样，把全部的知识当作条件b,那么b所对应的实验情境将是独特的，因而是不可重复的。于是主观主义者依主观概率做出的决策无异于豪赌，并非出于所谓的理性信念。②

与此相关的是两种解释的另一个细微而重要的区别。一方面，客观解释把整个概率陈述p(a,b)=r看成假说③,我们可以根据实验结果中的相对频率来检验这个假说④。因此，对于客观解释，a是什么并不重要，重要的是p(a,b)的值是多少，以及它是否与实验结果一致。⑤另一方面，主观解释则把a看成假说，把p(a,b)看成对假说a的置信度⑥;其中逻辑解释把概率陈述看成重言式或矛盾式，因而不接受经验检验⑦。波普尔认为主观解释是建立在逻辑解释的基础上的，因为“被全部知识b所支持的、对a的理性置信度”其实就是“b在逻辑上支持a的程度”。因此主观解释和逻辑解释一样把概率陈述p(a,b)=r看成逻辑公式，而且是无法被检验的重言式⑧,于是一切概率陈述都无法与经验证据建立联系。这就是主观解释的可检验性问题。⑨

还有一个问题与这个细微的区别有关。按照主观解释，第n次投硬币结果是正面向上的先验概率是二分之一；然而，如果大量实验的结果显示这个硬币是均匀的，根据这个实验证据所得的概率还是二分之一。波普尔认为主观解释无法解决这个悖论，因为它的基本假定就是理性置信度随着证据的积累发生线性的变化；但是在刚才的例子中，概率——也就是主观解释所说的置信度——并没有变化。对于客观解释，这个问题就很容易解决：因为客观解释的假设是整个概率陈述，而不是第n次实验结果这个事件；先前的实验证据必定会影响人们对第n次实验结果的估计，但只要证据与作为假设的整个概率陈述相一致，就不会影响这个假设，这就解释了刚才的例子中的概率并未因证据积累而变化的原因。(5)此外，如果我们把“全部的知识”等同于过去的一切实验证据，那么从确认度理论的角度看，在理论假设的条件下得出这些实验证据的概率恰好等于这些实验证据的先验概率，因此理论的确认度为零。这意味着，当我们的理论假设是概率陈述时，我们的全部知识与假设中的概率值毫无关系，因此概率不是主观知识或信念的度量。(11)

二、频率解释与量子力学解释

毋庸讳言，物理学对于波普尔的概率哲学有着重要的影响，他反对主观解释正是因为这种概率哲学不符合物理学对概率论的实际运用。(12)而且这种影响并不是单方面的，波普尔认为概率哲学在量子力学哲学当中的影响更不容忽视。他早在20世纪30年代就曾力图借助频率解释来处理量子力学不确定性原理的解释问题。

人们通常认为，不确定性原理是量子力学的基本原理之一。我们之所以无法同时测得微观粒子的精确位置和动量——也就是它们的“轨道”,正是因为这个原理的限制。(6)“轨道不能测得”又进一步意味着微观粒子不是实在的，即不是独立于我们的观察活动的。②波普尔强烈反对这样的观点。一方面，他认为某些特殊情况下的粒子轨道是可以测得的，例如先测位置再测动量，那么这两次测量之间的粒子轨道就可以很容易地计算出来。③而且他反复强调我们需要轨道的概念来验证不确定性原理，就像我们需要精确观察每一次投骰子的结果以验证相关的概率一样。(7)另一方面，他并不认为不确定性原理是量子力学的基本原理，因为我们可以从薛定谔方程和波恩几率诠释出发来推导不确定性原理，但是反过来显然无法推导。⑤这就意味着量子力学的统计特性并不是不确定性原理的结果，反倒是因为量子力学在根本上具有这种统计特性，所以才会导致不确定性原理。波普尔认为，按照频率解释，因为波恩几率诠释可以为单个粒子的测量结果赋予概率，所以它属于“形式上单称的概率陈述”(formally singular probability statement)⑥。于是，由波恩几率诠释推导出来的不确定性原理若用来描述单个粒子，显然也属于“形式上单称的概率陈述”。也就是说，当人们根据不确定性原理说“该粒子位置的不确定度与动量的不确定度的乘积不小于某个常数”时，他们并不是在讨论某一个粒子，而是大量同种粒子的测量结果构成的序列。因此，这句话的实际含义是——当我们从大量同种粒子当中筛选出位置处于某一范围的粒子时，它们的动量的不确定度与位置的不确定度的乘积不小于某个常数；当我们从大量同种粒子中筛选出动量值处于某一范围的粒子时，它们的位置的不确定度与动量的不确定度的乘积仍不小于那个常数。这就是波普尔对不确定性原理的统计解释。⑦

在波普尔看来，客观解释在量子力学哲学问题上的应用是成功的，而与之相反的则是主观解释的失败。波普尔一直强调的一个观点就是，概率性的结论(或称统计结论)只能从概率性的前提推导出来。⑧因为量子力学是一个统计理论，且不确定性原理是由这个统计理论推导出来的统计结论，所以我们不能用不确定性原理来解释量子力学的统计特性，特别是不能说不确定性原理限制了我们的知识，反倒应该说它增加了我们关于粒子分布规律的知识。(8)一般地，我们不能从主观前提推导出统计结论。概率的主观解释经常把“几乎确定”解释为客观的“几乎总是发生”而不是主观的“非常坚定地相信”,即主观解释在推导过程中把主观概率命题偷换成了客观概率命题，这显然不合法。(9)这种至少是不经意的偷换概念显然也影响了很多物理学家，使他们总在主观解释和客观解释之间摇摆(10),甚至认为量子力学根本不是对客观自然的表征而是对主观知识的表征。波普尔认为这种看法引入了概率的主观解释，从而不可避免地导致主观解释的诸多谬误。因此，我们必须通过客观解释重构量子力学哲学，只有这样才能得到正确的量子力学解释。(11)

三、从频率解释到倾向性解释

双缝干涉实验是波普尔关注的另一个量子力学哲学难题。在这个实验中，两条狭缝交替开放和同时开放所得的粒子分布明显不同。这一奇特事实让波普尔开始怀疑自己对单个事件概率的解释：既然波函数表征着单个粒子的概率，而双缝干涉实验显然意味着波函数可以相互干涉，那么单个事件的概率应当也是可以相互作用的，即是物理实在的，而不只是“形式上单称的概率陈述”。这个想法促使波普尔反思频率解释的不足，并于1953年放弃了它。(12)

为揭示频率解释的不足，波普尔构造了一个例子。有一个不均匀的骰子，大量实验表明用它掷出“六”的概率是四分之一。现在考虑一个由掷骰子的结果构成的序列b,其中三次结果是投掷正常骰子得到的，其余结果都是投掷那个不均匀的骰子得到的。事实上，投掷正常骰子得到“六”的概率是六分之一；但由于这个结果处在不均匀骰子占“统治地位”的序列中，根据频率解释，我们只能说其中投掷正常骰子得到“六”的概率是四分之一。⑤

人们可能会说，投掷正常骰子的结果不仅属于序列b,它们也属于仅由投掷正常骰子的结果构成的序列c。然而，如果我们讨论的是这两个序列的公共部分，那么该部分只有三个元素，我们显然无法在只有三个元素的序列中得到“六分之一”这个频率。因此我们只能考虑b和c这两个序列。而且，之所以投掷正常骰子得到“六”的概率是六分之一，是因为我们必须在序列c中——而不能在序列b中——计算该事件的频率。这说明与骰子有关的物理属性决定了我们必须采纳何种序列中的频率作为概率，在一般情况下，则是特定的实验条件决定了特定事件的概率。其中“实验”所言说的虽然是一个单个的实验，但必须相对于这个实验的同一性标准。这种同一性标准指的是把两次实验看作同一种实验的标准，例如投硬币的时候需要投多高，投两米高和投十米高算不算是同一种投硬币的实验。这样的同一性标准得到确立之后，实际上一种客观的实验条件或者实验设置就确立起来了。所谓概率，就是实验条件的属性，它所刻画的是实验条件产生特定事件的一种物理的、真实的倾向性。这就是波普尔提倡的概率的倾向性解释。(13)

频率解释在理论上还有一个弱点，即理想序列的无限性，这导致它对概率与现实序列中相对频率的联系问题的处理难以令人完全满 意。(14)波普尔认为建立在测度论基础上的“新古典概率论”可以近乎完美地解决这个问题。③更 重要的是，在这个理论中，概率被赋予单个事件，具体的概率值与该事件的客观条件密切相关，这恰好符合倾向性解释的主 张。④

在波普尔看来，倾向性这种物理的、真实的属性与物理学中的力、场等概念别无二致。我们可以考虑一个关于电场的物理陈述，若引入一个带电体，我们就可以通过带电体的受力情况来检验关于电场的陈述。但这个陈述并不是关于带电体的，而是关于电场的倾向性的。同理，我们可以通过投骰子来检验其概率，但这个概率陈述并不是关于骰子的，而是关于实验条件的倾向性的。如果我们在非常弱的引力场中投掷上述不均匀的骰子，那么得到“六”的概率就可能从四分之一减小到六分之一；如果该引力场变得非常强，那么相应的概率就可能上升到三分之一甚至二分之一。(15)波普尔认为倾向性与力、场的类比是非常完美的，然而由于倾向性与亚里士多德的“潜能”(Potentia)非常相似，人们很容易误以为倾向性与“潜能”一样，都是事物的内禀属性。事实上，倾向性是实验条件对事物的物理作用，因此它刻画的是二者之间的关系；就像力不是某物的内禀属性而是两个物体之间的相互作用一样，倾向性也是一种关系属性，而不是内禀属性。(16)

为了更具体地说明倾向性是真实的物理性质，波普尔举了钉板和小球的例子。小球从钉板顶部滚落，与钉子发生一系列碰撞之后落入钉板下方的格子里；当大量小球从同一个起点滚落之后，它们最终的落点会呈现一种正态分布：落在起点正下方的小球最多，落在旁边格子里的小球随着它到起点正下方的距离的增大而减少。在波普尔看来，小球落入某个格子的概率，也就是倾向性，是钉板这个实验设置的真实的物理性质。所谓真实的物理性质，也就是说它可以被改变，当我们改变它时，它将会做出相应的反应。对于钉板而言，我们要改变与之相关的倾向性，就可以把它倾斜着摆放；对于我们的操作，实验结果的倾向性会立刻做出反应——小球落点的分布会发生倾斜。这意味着，实验设置发生改变时，实验结果的倾向性也随之变化，因此，倾向性是一种真实的物理性质。(17)

四、倾向性解释与量子力学解释

如前所述，正是量子力学哲学使波普尔放弃频率解释并转向倾向性解释(18),这是量子力学哲学影响概率哲学的又一个典型案例。反过来，倾向性解释作为新的概率哲学必定也要深刻地影响量子力学哲学。

在量子力学实验中，流行的说法认为微观物理系统的波函数所对应的概率分布在该系统被测量时以一种随机的、非连续的方式突变成另一种概率分布，即“波包坍缩”,而且这是微观物理系统特有的性质。波普尔则认为波函数是倾向性的数学表征，称其为“倾向波”。(19)量子力学与经典力学的根本不同在于“倾向波”可以相互干涉，这说明“倾向波”是物理实在的④,但除此之外二者并没有太大的区别。如果我们把概率理解为倾向性，那么，量子力学实验与钉板小球实验同样作为概率性的过程，其中呈现的倾向性也应当是同质的；“波包坍缩”并不仅是微观现象，它其实无非是倾向性的转变。

作为例子，波普尔试图说明“波包坍缩”在钉板小球的实验中也是存在的：如果我们选定钉板上的一颗钉子，并且仅考虑下落过程中与这颗钉子发生碰撞的小球，那么这些小球的分布自然和全部小球的分布有所不同；但我们并不会说小球在与这颗钉子发生碰撞的瞬间发生了“波包坍缩”,以至于碰撞之后的分布较碰撞之前发生了变化。应该说，当我们仅考虑与这颗钉子发生碰撞的小球时，实验设置(即同一性标准)发生了改变，因此倾向性随之改变，最终呈现出不同的分布。同样地，当双缝干涉实验中的一条狭缝开放或关闭时，实验设置的改变也会导致粒子的不同概率分布。(20)这时人们总是疑惑穿过其中一个狭缝的粒子怎么知道另一个狭缝是否是开着的。波普尔认为粒子确实无法知道，但整个实验装置“知道”究竟哪条缝是开着的，因此是实验设置决定了粒子的分布。⑥在另一个实验中，一个光子射向半反半透的镜子。不妨设这个光子出现在反射的光路上，此时我们不应该说这个光子发生了“波包坍缩”,不能说它被反射的概率从二分之一突然变成了一，它被透射的概率从二分之一突然变成了零；而应该说当我们仅考虑被反射的光子时，实验设置发生了变化，倾向性也随之发生了变化，因此我们得到了与之前完全不同的分布。(21)这样看来，“波包坍缩”和主观解释所犯的错误如出一辙。主观主义者认为新“信息”可以改变概率，例如得知骰子点数是偶数时，点数是二的概率就由六分之一变成了三分之一。但波普尔认为这只是改变了p(a,b)中的b,即采纳不同的同一性标准，把结果是奇数的实验与结果是偶数的实验区别开，把后者看成b,相当于改变了实验设置。因此概率的变化仍是由客观的原因——而不是知识或信念的变化——导致的。(22)

在这里，波普尔明确表示反对哥本哈根解释的观点。作为哥本哈根学派的代表人物之一，海森堡曾把“波包坍缩”说成是“观察者”从可能性中挑选出现实性的过程。(23)在波普尔看来，海森堡的错误恰恰在于错误的概率哲学。海森堡认为，作为一种新的“客观的”物理实在，量子力学中的概率正是被量化了的亚里士多德的“潜能”概念。④然而，正如前文提到的，波普尔认为正是亚里士多德的本质主义使人们习惯于把关系属性看成是“观念的”(ideal)而不是“实在的”(real),这种习惯导致他们把倾向性这种关系属性看成是主观的东西，这就是概率的主观解释的思想根源。(24)而把概率当成内禀于对象之中的性质，而不是对象与其环境之间的关系，正是导致种种量子疑难的重要诱因之一。(25)

尽管波普尔终其一生从未放弃他的倾向性解释，但仍有很多学者不赞同这种观点。(26)费耶阿本德认为量子物理学的新颖之处在于概率并不直接等于波函数的“函数值”,而是“函数值”的“模平方”,这才导致了量子干涉现象。可是波普尔并不能通过钉板的类比来解释干涉现象，因为尽管干涉现象确实与实验设置有关，但问题并不在这里，而是在于我们无法在承认粒子轨道这个概念的前提下解释干涉现象。以N.玻尔(Niels Bohr)为代表的哥本哈根解释正是在充分考虑到这些问题的基础上才最终放弃轨道概念的。(27)然而波普尔提出钉板实验的目的并非解释干涉现象，而且他很清楚钉板实验和双缝实验的区别(28),但他认为这种区别是次要的，二者的相同点才是所谓“波包坍缩”的本质。(29)至于粒子轨道的概念，费耶阿本德的论证代表着被物理学家广泛接受的正统量子力学解释，但这种解释并非没有问题。正如波普尔指出的，玻尔认为位置和动量只能在相互排斥的实验设置中得到测量，但事实上对动量的测量结果往往是通过对位置的测量而计算出来的。(30)在数学上，人们在发现一般的希尔伯特空间中同时对应精确的位置和动量的状态矢量不存在后，都开始相信单个粒子不能同时具有位置和动量。(31)但波普尔和玻尔、爱因斯坦等物理学家一样反对这种“毕达哥拉斯主义”,他明确表示：状态矢量仅代表系统的统计特性，并不描述单个粒子，因此与粒子的精确位置与动量不冲突。(32)

费耶阿本德在仔细梳理玻尔的思想脉络之后总结道，要解决量子力学解释问题，还是得回归玻尔及其互补性原理。(33)然而现实却并未接受他的建议，否则我们现在就不会看到那么多互不相容的量子力学解释。有趣的是，众多量子力学解释并存的事实也可以用来反驳波普尔的观点，因为把量子力学解释问题完全看成概率解释问题显然也不是一个完美的方案。尽管我们可以利用概率解释保留粒子轨道的概念，进而通过真实的物理相互作用来解释不确定性，但这种解释与量子力学的数学结构之间的冲突仍是不容忽视的。即便不是毕达哥拉斯主义者，也必须严肃对待这个冲突。巴布在其批评波普尔的倾向性解释的文章中所强调的正是这个解释与量子概率的数学特性不一致的问题。(34)不过这篇文章侧重于对量子概率的说明，没有明确指出波普尔究竟在哪个环节犯了错误。实际上，量子概率、量子逻辑的演算系统都与量子力学有着同样的数学结构。我们将会看到，波普尔概率哲学的问题在他关于量子逻辑的论述中表现得最为突出。

五、量子逻辑及其概率特性

这里所说的量子逻辑指的是由伯克霍夫和冯·诺依曼在1936年提出的一项与量子力学的数学基础相关的研究。(35)他们在研究中指出，无论是经典物理学还是量子物理学，在关于物理系统的性质命题和描述该物理系统的状态空间的特定部分(子集或子空间)之间都可以建立一种对应关系，而且这种对应关系又可以把命题演算和状态空间的类似演算对应起来。如果说命题演算使那些物理学命题构成了一个逻辑系统，那么相应的状态空间以及相关的演算就构成了与这个逻辑系统同构的代数结构。通过对比经典物理学和量子物理学对应的代数结构，在数学上不难发现，经典物理学对应的代数结构是布尔代数，其中“布尔和”与“布尔积”之间的分配律是成立的，而量子物理学对应的代数结构中却存在着违背分配律的情况。分配律是否成立是区别这两种代数结构的唯一特征。(36)

代数结构上的差异似乎意味着量子力学的逻辑不同于经典力学的逻辑，也就是经典逻辑，这当然涉及两种逻辑系统的地位和关系等逻辑哲学问题。以普特南为代表的一些学者主张量子逻辑是经典逻辑背后的“真逻辑”,并用量子逻辑构造新的量子力学解释。(37)波普尔对这种逻辑哲学和量子力学解释深感不满(38),但他在讨论量子逻辑问题时却没有以逻辑哲学理论为切入点，而是试图论证所谓的分配律不成立是由于伯克霍夫和冯·诺依曼忽略了关于概率的一些基本前提，如果我们把这些前提考虑进来，则很容易证明分配律是成立的。也就是说，量子力学对应的数学结构也是布尔代数，它与经典力学并没有那么大的差别。

波普尔所说的与概率有关的前提，指的是当我们在一种代数结构上定义一个被理解为概率的函数时，这个函数必须要满足的条件。设a和b为某种代数结构中的元素，m(x)为这种代数结构上的“概率函数”,波普尔认为m(x)必须满足一些条件，例如：

R1-2:a=b当且仅当对于任意m(x)都有m(a)=m(b);R4:对于任意m(x)都有m(a)+m(b)=m(a∧b)+m(a∨b)。

其中“∧”和“∨”分别是这种代数结构中与“布尔积”和“布尔和”相对应的运算。在伯克霍夫和冯·诺依曼所考虑的那些代数结构中，都存在着一个“最大”元素“1”和一个“最小”元素“0”,如果a和b满足a∧b=0并且a∨b=1,就说它们互为“补元”(complement)。波普尔注意到冯·诺依曼在其他论著中曾经证明过这个定理：如果一个代数结构中每一个元素都有唯一的补元，并且还满足一些其他的条件[特别是模条件(modular law)],那么这个代数结构就是布尔代数。然而，考虑到R1-2、R4等前提，波普尔认为伯克霍夫和冯·诺依曼所考虑的代数结构必定要满足这些条件。假设b和c都是a的补元，由R4得：对于任意m(x)都有m(b)=m(a∧b)+m(a∨b)-m(a)=m(0)+m(1)-m(a)=m(a∧c)+m(a∨c)-m(a)=m(c),再由R1-2即可得到b=c,这就是补元的唯一性。紧接着，波普尔又利用类似的方法证明了(包括模条件在内的)其他的条件，于是他认为伯克霍夫和冯·诺依曼所讨论的量子力学的代数结构仍然是布尔代数，所以量子力学的逻辑结构也没有偏离经典逻辑。(39)

波普尔的论证看起来很有道理，而且非常严谨，但并不正确。主要的问题在于R4这个条件过分严格——伯克霍夫和冯·诺依曼的讨论只要求存在一个m(x)满足R4中的等式，并不要求这个等式对任何m(x)都成立。因此波普尔在证明过程中得到的m(b)=m(c)并不是对所有的m(x)都成立的，并不能借助R1-2得到补元的唯一性，即b=c。(波普尔在对模条件的证明中犯了同样的错误。)事实上，伯克霍夫和冯·诺依曼也从来没有认为他们所讨论的代数结构中的每个元素都有唯一的补元，因此波普尔的理解和证明都是错误的。(40)

波普尔的上述论证显然是在借助概率的性质来推导逻辑规律，他之所以采用这样的方法是因为他相信概率对于逻辑确实有这样的规定作用。早在20世纪30年代，波普尔就曾提出一个“最小的”概率演算公理系统，即所有的概率解释都至少应该承认这个公理系统，进而证明确认度不满足这些公理，所以不是概率。(41)在这个系统中，涉及补元的公理是：如果p(b,b)=p(c,b)并不对所有的c都成立，那么p(a,b)+p(a¯,b)=p(b,b)。④假设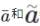都是a的补元，那么根据这个公理我们很容易证明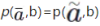对所有的b都成立，进而得到补元的唯一性，即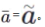不仅如此，波普尔还明确指出，满足他的公理系统的所有元素(a、b、c等等)恰好构成一个布尔代数。(42)这意味着一个概率演算体系的最低标准也必须“内嵌”着代表经典逻辑的布尔代数，当然也必然要求补元有唯一性。我们注意到，波普尔在评判概率的逻辑解释时曾主张，只有当布尔代数从概率演算规则中推导出来时，人们才能说逻辑解释是合理的。(43)相信他在写这段话时想到的一定是他的概率系统。难怪他要不遗余力地“证明”以非布尔代数为基本结构的量子逻辑的“错误”。

事实上，这样的“证明”只要不在数学上犯错误，就一定是由某些基本设定的分歧所导致的。波普尔的概率公理系统的一个基本假设是，如果a和b都是该系统所讨论的元素，那么它们的“积”(product)ab也是系统所讨论的元素。与之相关的公理是p(ab, c)=p(a, bc)p(b, c)。③显然，这预设了任意两个命题的合取式的存在，因此是哥本哈根解释不能允许的。例如a是关于某粒子位置的命题，b是关于该粒子动量的命题，哥本哈根解释认为a和b不能同时有意义，所以它们的积ab自然不会有定义。波普尔则认为微观粒子的任意精确的动量和位置是同时存在的，上述假设和公理正是这一信念的集中体现，也是与量子力学的数学结构之间冲突的焦点。

前文曾提到，波普尔把条件概率p(a, b)作为最基本的概念；然而在通常的概率体系中，绝对概率才是最基本的概念，且当b的绝对概率p(b)为零时，p(a, b)是无意义的。波普尔认为通常的设定存在缺陷。根据他的看法，全称命题不可被证实，因此其概率和逻辑矛盾的概率一样，都是零；可是，当b是一个全称命题，a是b的逻辑推论时，p(a, b)等于1,显然是有意义的。波普尔的系统恰好能够容许这种条件概率。④作为系统的定理，波普尔证明，若将b替换成逻辑矛盾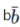(即“b并且非b”),则p(a,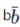)=1。⑤现在我们来构造一个例子：设|u〉、|v〉、|w〉是三个线性无关的单位态矢量，〈u|v〉=0。用a、b、c分别代表投影算符|u〉〈u|、|u〉〈u|+|v〉〈v|、|w〉〈w|所对应的命题，也代表系统希尔伯特空间中相应的子空间。易知ab=a, 且由线性无关性可知bc对应的子空间是{0},因此它等价于逻辑矛盾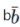,所以p(a,bc)=p(a,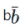)=1。假定适当选择|v〉即可得到p(a, c)≠p(b, c),则p(ab, c)=p(a, c)≠p(b, c)=p(a, bc)p(b, c),这与波普尔的公理矛盾。

值得注意的是，在上述例子中，b与c既不正交又没有非平庸的公共部分，它们对应的可观测量与位置和动量一样是不相容的。然而，正是因为它们不相容，所以在目前的量子力学数学体系中二者的联合概率分布(joint probability distribution)不存在。因此，我们并不能先借助公认的数学模型、根据联合概率计算出p(b, c),再由p(b, c)的计算结果推论出“适当选择|v〉即可得到p(a, c)≠p(b, c)”这个结论。我们只能说，“对任何|v〉都有p(a, c)=p(b, c)”是不太可能的，或者猜测p(a, c)和p(b, c)分别与a、c和b、c之间的转化概率有关，后两者分别为tr(ac)=|〈u|w〉和tr(bc)=|〈u|w〉+|〈v|w〉,只要〈v|w〉≠0就能保证这两个转化概率不相等。无论如何，粗暴地断言波普尔的“错误”都是不可取的。可以说，这个细节更加深刻地揭示了同时承认不相容可观测量的理论与量子力学的数学结构之间不容忽视的张力。萨普斯在评价波普尔的量子力学哲学的文章中提到，尽管他非常赞同波普尔对量子逻辑的反驳(44),但仍认为不相容可观测量的联合概率分布与量子力学的数学结构之间的冲突是个非常棘手的问题②。波普尔在回应文章中承认自己忽略了这个问题，并认为这个问题超出了他的能力范围。但他仍坚持认为他的量子力学哲学与量子力学数学基础之间的冲突并不意味着他的失败，因为我们总是有可能构造适当的新理论来替代现有的、冯·诺依曼式的数学模型，至少是绕开联合概率分布的问题。(45)作为一个公正客观的总结，我们应当认识到现实情况并不支持波普尔的构想，同时也不能武断地否认该构想的可能性。

六、结语

波普尔在量子力学诞生初期就敏锐地意识到它与概率解释的深刻联系，并在其整个学术生涯中始终如一地坚持把概率解释的方法应用在包括量子逻辑在内的量子力学解释问题中。前文的论证表明，概率解释不仅影响了波普尔的量子力学解释，而且渗透在他的逻辑思想当中；后者导致他坚决反对建立在量子逻辑基础上的量子力学解释，这可视作经典概率解释对量子力学解释的一种负面影响。诚然，他的概率解释方法并没有成功地兼顾所有的量子疑难，在这个意义上他失败了。可是如果我们要求一种量子力学解释同时解决所有相关问题，那么包括哥本哈根解释在内的一切现有的理论都是失败的。比起否定甚至嘲弄波普尔的失败，我们更应该仔细考察概率解释与量子力学解释之间的相互影响，以加深对物理学、概率论和逻辑学的基本结构的理解。波普尔的不懈努力为我们展示出这种结构的脉络，我们可以通过他的工作更全面地把握量子力学及其概率特性。无论未来这些领域会如何发展，对当前状况的深入研究都将起到至关重要的作用。

【注释】

① Cf.Donald Gillies,“Popper's Contribution to the Philosophy of Probability”,in Karl Popper:Philosophy and Problems,Anthony O'Hear ed.,Cambridge University Press,1995,p.103.

(1) 限于篇幅,我们对波普尔批评主观解释的诸论证不加评判。

(2) ③⑥ Cf.Karl R.Popper,The Logic of Scientific Discovery,Routledge,1959,pp.403-405;pp.135-137;pp.159-163.

(3) ⑤⑦ Cf.Karl R.Popper,Realism and the Aim of Science,Hutchinson,1983,pp.289-290;pp.297-298;pp.299-300.

(4) ②③④⑤⑥⑦⑧⑨ Cf.Karl R.Popper,Realism and the Aim of Science,Hutchinson,1983,p.315;pp.310-312;p.296;p.288,p.294;p.312;p.296;pp.293-294;p.296;pp.337-339.

(5) (11)(12) Cf.Karl R.Popper,The Logic of Scientific Discovery,Routledge,1959,pp.425-427;pp.431-432;p.137.

(6) ②③⑤⑥⑦⑧ Cf.Karl R.Popper,The Logic of Scientific Discovery,Routledge,1959,p.223;p.227;p.214,p.226;p.218;pp.202-203;pp.219-220;p.243,sect.70.

(7) Cf.Karl R.Popper,The Logic of Scientific Discovery,Routledge,1959,pp.226-227;Karl R.Popper,Quantum Theory and the Schism in Physics,Hutchinson,1982,pp.145-147.

(8) Cf.Karl R.Popper,“Quantum Mechanics without the Observer”,in Quantum Theory and Reality,Mario Bunge ed.,Springer-Verlag,1967,pp.20-21.

(9) Cf.Karl R.Popper,The Logic of Scientific Discovery,Routledge,1959,pp.171-172;Karl R.Popper,“Quantum Mechanics without the Observer”,in Quantum Theory and Reality,Mario Bunge ed.,Springer-Verlag,1967,pp.29-30.

(10) Cf.Karl R.Popper,Quantum Theory and the Schism in Physics,Hutchinson,1982,pp.106-118.

(11) Cf.Karl R.Popper,The Logic of Scientific Discovery,Routledge,1959,pp.229-230.

(12) ⑤ Cf.Karl R.Popper,“The Propensity Interpretation of Probability”,The British Journal for the Philosophy of Science 37(1959):pp.27-28;pp.31-32.

(13) Cf.Karl R.Popper,“The Propensity Interpretation of Probability”,The British Journal for the Philosophy of Science 37(1959):pp.32-35;Karl R.Popper,“Quantum Mechanics without the Observer”,in Quantum Theory and Reality,Mario Bunge ed.,Springer-Verlag,1967,pp.38-39.

(14) ③④ Cf.Karl R.Popper,Realism and the Aim of Science,Hutchinson,1983,pp.367-370;pp.384-387;pp.387-390.

(15) Cf.Karl R.Popper,“The Propensity Interpretation of the Calculus of Probability,and the Quantum Theory”,in Observation and Interpretation:A Symposium of Philosophers and Physicists,Stefan Körner ed.,Butterworth,1957,p.68.

(16) Cf.Karl R.Popper,“The Propensity Interpretation of Probability”,The British Journal for the Philosophy of Science 37(1959):pp.37-38;Karl R.Popper,“Quantum Mechanics without the Observer”,in Quantum Theory and Reality,Mario Bunge ed.,Springer-Verlag,1967,pp.39-40;Karl R.Popper,Realism and the Aim of Science,Hutchinson,1983,p.359.

(17) ⑥ Cf.Karl R.Popper,“Quantum Mechanics without the Observer”,in Quantum Theory and Reality,Mario Bunge ed.,Springer-Verlag,1967,p.33;p.24.

(18) Cf.Karl R.Popper,Realism and the Aim of Science,Hutchinson,1983,p.398.

(19) ④ Cf.Karl R.Popper,Quantum Theory and the Schism in Physics,Hutchinson,1982,p.126;p.84.

(20) Cf.Karl R.Popper,“The Propensity Interpretation of the Calculus of Probability,and the Quantum Theory”,in Observation and Interpretation:A Symposium of Philosophers and Physicists,Stefan Körner ed.,Butterworth,1957,p.69.

(21) Cf.Karl R.Popper,The Logic of Scientific Discovery,Routledge,1959,pp.231-232;Karl R.Popper,“Quantum Mechanics without the Observer”,in Quantum Theory and Reality,Mario Bunge ed.,Springer-Verlag,1967,pp.34-37.

(22) Cf.Karl R.Popper,Realism and the Aim of Science,Hutchinson,1983,p.394.

(23) ④ Cf.Werner Heisenberg,“The Development of the Interpretation of the Quantum Theory”,in Niels Bohr and the Development of Physics,Wolfgang Pauli ed.,Pergamon Press Ltd.,1955,p.23;pp.12-13.

(24) Cf.Karl R.Popper,Quantum Theory and the Schism in Physics,Hutchinson,1982,p.128.

(25) Cf.Karl R.Popper,“Quantum Mechanics without the Observer”,in Quantum Theory and Reality,Mario Bunge ed.,Springer-Verlag,1967,p.19.

(26) 大多数反驳属于概率哲学,不涉及量子力学解释。[Cf.David Hugh Mellor,The Matter of Chance,Cambridge University Press,1971,pp.63-82;Paul Humphreys,“Why Propensities Cannot Be Probabilities”,The Philosophical Review XCIV(1985):pp.557-570;Peter J.Clark,“Statistical Mechanics and the Propensity Interpretation of Probability”,in Chance in Physics,Jean Bricmont,Giancarlo Ghirardi,Detlef Dürr,Francesco Petruccione,Maria Carla Galavotti & Nino Zanghi eds.,Springer,2001,pp.271-281;Antony Eagle,“Twenty-one Arguments against Propensity Analyses of Probability”,Erkenntnis 60(2004):pp.371-416;Manuel Bächtold,“An Instrumentalist Criticism of Popper's Propensity”,in Karl Popper.A Centenary Assessment.Volume III:Science,Ian C.Jarvie,Karl M.Milford & David W.Miller eds.,Ashgate,2006,pp.97-104;Jacob Rosenthal,“Karl Popper's Propensity Interpretation of Probability”,in Karl Popper.A Centenary Assessment.Volume III:Science,Ian C.Jarvie,Karl M.Milford & David W.Miller eds.,Ashgate,2006,pp.105-112.]

(27) Cf.Paul K.Feyerabend,“On a Recent Critique of Complementarity:Part I”,Philosophy of Science 35(1968):pp.324-329;Paul K.Feyerabend,“On a Recent Critique of Complementarity:Part II”,Philosophy of Science 36(1969):pp.94-97.

(28) Cf.W.W.Bartley,Ⅲ,“Critical Study:The Philosophy of Karl Popper,Part II:Consciousness and Physics”,Philosophia 7(1978):p.695.

(29) Cf.Karl R.Popper,Quantum Theory and the Schism in Physics,Hutchinson,1982,p.88.

(30) Cf.Karl R.Popper,“Quantum Mechanics without the Observer”,in Quantum Theory and Reality,Mario Bunge ed.,Springer-Verlag,1967,pp.23-24;Karl R.Popper,Quantum Theory and the Schism in Physics,Hutchinson,1982,pp.142-143;Leslie E.Ballentine,“The Statistical Interpretation of Quantum Mechanics”,Reviews of Modern Physics 42(1970):pp.365-366.

(31) 这些反实在论者的论据还包括贝尔不等式、柯申—斯派克定理(Kochen-Specker Theorem)等,但这些理由仍不足以反驳实在论。具体可参见量子力学统计解释的相关研究,例如,Hans Rudolf Tschudi,“The Statistical Interpretation of Quantum Mechanics”,https://zenodo.org/records/15078174(Mar 25,2025)。

(32) Cf.Karl R.Popper,“Quantum Mechanics without the Observer”,in Quantum Theory and Reality,Mario Bunge ed.,Springer-Verlag,1967,pp.25-26.

(33) Cf.Paul K.Feyerabend,“On a Recent Critique of Complementarity:Part II”,Philosophy of Science 36(1969):pp.103-104.

(34) Cf.Jeffrey Bub,“Popper's Propensity Interpretation of Probability and Quantum Mechanics”,retrieved from the University of Minnesota Digital Conservancy.http://hdl.handle.net/11299/184671.

(35) Cf.Garrett Birkhoff & John von Neumann,“The Logic of Quantum Mechanics”,Annals of Mathematics 37(1936):pp.823-843.

(36) 参见叶峰:《量子逻辑》,载《方法论全书(II):应用逻辑学方法》,李志才主编,南京大学出版社,1998,第457—505页。

(37) Cf.Hilary Putnam,“Is Logic Empirical?”,in Boston Studies in the Philosophy of Science,vol.5,Robert S.Cohen & Marx W.Wartofsky eds.,Reidel,1968,pp.216-241.

(38) Cf.Flavio Del Santo,“An Unpublished Debate Brought to Light:Karl Popper's Enterprise against the Logic of Quantum Mechanics”,Studies in History and Philosophy of Science Part B:Studies in History and Philosophy of Modern Physics 70(2020):p.69.

(39) Cf.Karl R.Popper,“Birkhoff and von Neumann's Interpretation of Quantum Mechanics”,Nature 219(1968):pp.683-684.

(40) Cf.Erhard Scheibe,“Popper and Quantum Logic”,The British Journal for the Philosophy of Science 25(1974):pp.321-325.

(41) ④ Cf.Karl R.Popper,The Logic of Scientific Discovery,Routledge,1959,p.319;p.337.

(42) ③④⑤ Cf.Karl R.Popper,The Logic of Scientific Discovery,Routledge,1959,p.365;p.337;pp.333-335;p.335,p.361.

(43) Cf.Karl R.Popper,Realism and the Aim of Science,Hutchinson,1983,p.293.

(44) ② Cf.Patrick Suppes,“Popper's Analysis of Probability in Quantum Mechanics”,in The Philosophy of Karl Popper,Book II,Paul A.Schilpp ed.,The Open Court Publishing Co.,1974,p.768;pp.771-774.

(45) Cf.Karl R.Popper,“Replies to My Critics”,in The Philosophy of Karl Popper,Book II,Paul A.Schilpp ed.,The Open Court Publishing Co.,1974,pp.1138-1139.

原载：《世界哲学》2025年第4期